Identify the Function Family to Which G Belongs

Require whatsoever homework assistance to solve the linear functions questions? If yes, and so refer to this article thoroughly. Here, we have fabricated available a grooming guide ie., Big Ideas Math Algebra 2 Answers Chapter one Linear Functions which helps you improve your math proficiency. Answer all your questions and articulate your complex queries regarding BIM Alegra ii Reply Primal Chapter 1 Linear Functions topics. Ace upwardly your grooming by taking help from Big Ideas Math Algebra ii Answers and learn the concepts from Exercises Questions, Review Tests, Chapter Tests, Cumulative Assessments, etc.

Big Ideas Math Book Algebra two Answer Key Chapter 1 Linear Functions

Scoring good grades in any of your exams can make you lot attain what y'all are looking for but improving your subject knowledge make you invent a new thing that you dreamt of. So, acquire and exercise all the concepts covered in BIM Algebra ii Answer Fundamental Ch 1 Linear Functions to enhance subject knowledge and increase your math skills. Big Ideas Math Book Algebra 2 Chapter ane Solutions is the all-time cloth for you all to prepare & score well in the exams. Therefore, click on the links and kickstart your preparation.

• Linear Functions Maintaining Mathematical Proficiency – Folio one
• Linear Functions Maintaining Mathematical Practices – Page ii
• Lesson ane.1 Parent Functions and Transformations – Folio (4-10)
• Parent Functions and Transformations 1.i Exercises – Folio (8-10)
• Lesson 1.2 Transformations of Linear and Absolute Value Functions – Page (12-18)
• Transformations of Linear and Absolute Value Functions 1.2 Exercises – Page (xvi-18)
• Linear Functions Report Skills Taking Command of Your Class Time – Page xix
• Linear Functions one.1-1.2 Quiz – Page 20
• Lesson ane.three Modeling with Linear Functions – Page (22-28)
• Modeling with Linear Functions ane.three Exercises – Page (26-28)
• Lesson 1.four Solving Linear Systems – Page (30-36)
• Solving Linear Systems ane.iv Exercises – Page (34-36)
• Linear Functions Performance Task: Hugger-mugger of the Hanging Baskets – Page 37
• Linear Functions Chapter Review – Folio (38-twoscore)
• Linear Functions Affiliate Exam – Page 41
• Linear Functions Cumulative Assessment – Page (42-43)

Linear Functions Maintaining Mathematical Proficiency

Evaluate.

Question 1.
v • two³ + 7

five • two^three + seven
5.8+vii
xl+seven
47

Question two.
4 – 2(iii + 2)²

4 – two(3 + 2)ⁱⁱ
4 – ii (25)
4  – ii (25)
4 – l
= – 46

Question 3.
48 ÷ 4² + \(\frac{3}{v}\)

Question four.
50 ÷ v^two • two

50 ÷ five² • 2
50 ÷ 25 . 2
two .2
4

Question 5.
\(\frac{1}{2}\)(2^two+ 22)

Question 6.
\(\frac{one}{6}\)(6 + eighteen) – 2^two

Graph the transformation of the figure.

Question 7.
Translate the rectangle 1 unit right and four units up.

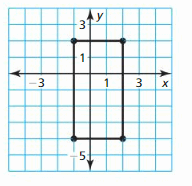
Question 8.
Reflect the triangle in the y-axis. Then translate 2 units left.

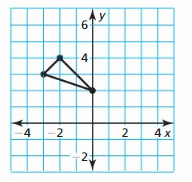
Question 9.
Translate the trapezoid 3 units down. Then reflect in the x-centrality.

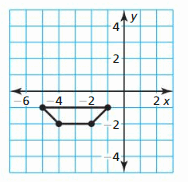
Question 10.
ABSTRACT REASONING Give an instance to testify why the lodge of operations is important when evaluating a numerical expression. Is the guild of transformations of figures important? Justify your answer.

Theorder of operations tells the states theguild to solve steps inexpressions with more than oneoperation. First, we solve whatsoeveroperations inside of parentheses or brackets.

Linear Functions Maintaining Mathematical Practices

Monitoring Progress

Utilize a graphing calculator to graph the equation using the standard viewing window and a square viewing window. Describe whatsoever differences in the graphs.

Question 1.
y = 2x – 3

Question ii.
y = | ten + ii |

Question three.
y = -x^two + 1

Question 4.
y = \(\sqrt{x-1}\)

Question 5.
y = 10^three – 2

Question 6.
y = 0.25x³

Decide whether the viewing window is foursquare. Explain.

Question 7.
-8 ≤ 10 ≤ 8, -2 ≤ y ≤ 8

Question 8.
-vii ≤ x ≤ 8, -2 ≤ y ≤ 8

Question 9.
-half-dozen ≤ ten ≤ nine, -2 ≤ y ≤ 8

Question ten.
-2 ≤ x≤ two, -3 ≤ y ≤ 3

Question 11.
-iv ≤ x ≤ 5, -iii ≤ y ≤ 3

Question 12.
-4 ≤ x ≤ 4, -3 ≤ y ≤ three

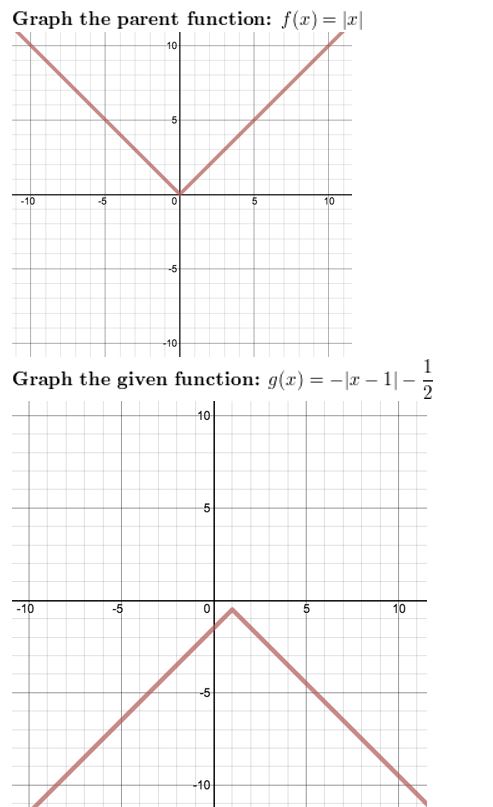
Lesson ane.1 Parent Functions and Transformations

Essential Question

What are the characteristics of some of the basic parent functions?
Odd. Cease behavior get in different directions. If afunction is positive, the left side of the graph volition signal down and the right side volition point up (increasing from left to right).

EXPLORATION one
Identifying Basic Parent Functions
Work with a partner. Graphs of viii basic parent functions are shown below. Classify each role as abiding, linear, accented value, quadratic, square root, cubic, reciprocal, or exponential. Justify your reasoning.

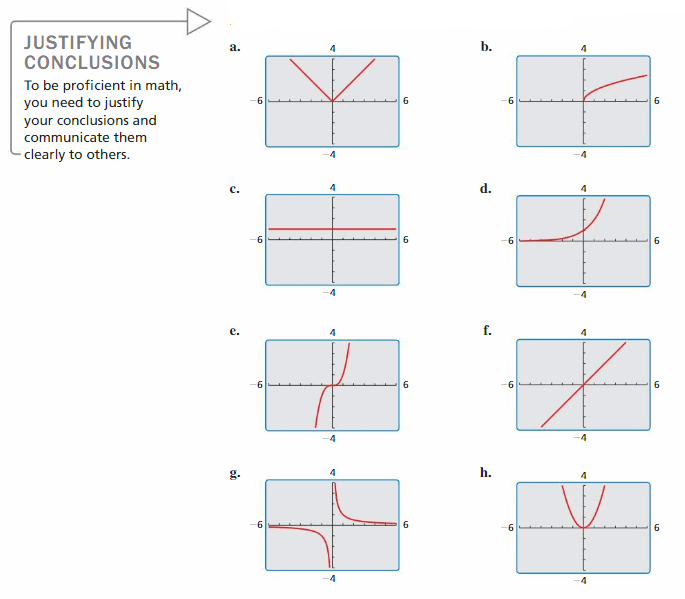
Communicate Your Answer

Question two.
What are the characteristics of some of the bones parent functions?
Central common points of linear parent functions include the fact that the: Equation is y = 10. Domain andrange are real numbers. Slope, or rate of change, is constant.

Question three.
Write an equation for each function whose graph is shown in Exploration 1. Then employ a graphing figurer to verify that your equations are right.

1.1 Lesson

Monitoring Progress

Question 1.
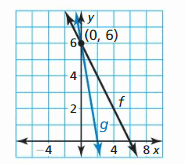
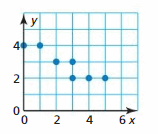
Identify the office family unit to which m belongs. Compare the graph of g to the graph of its parent part.

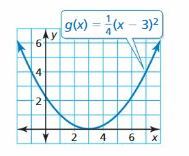
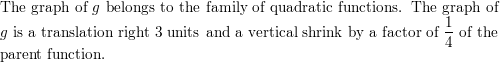
Graph the function and its parent function. Then describe the transformation.

Question 2.
yard(x) = x + 3

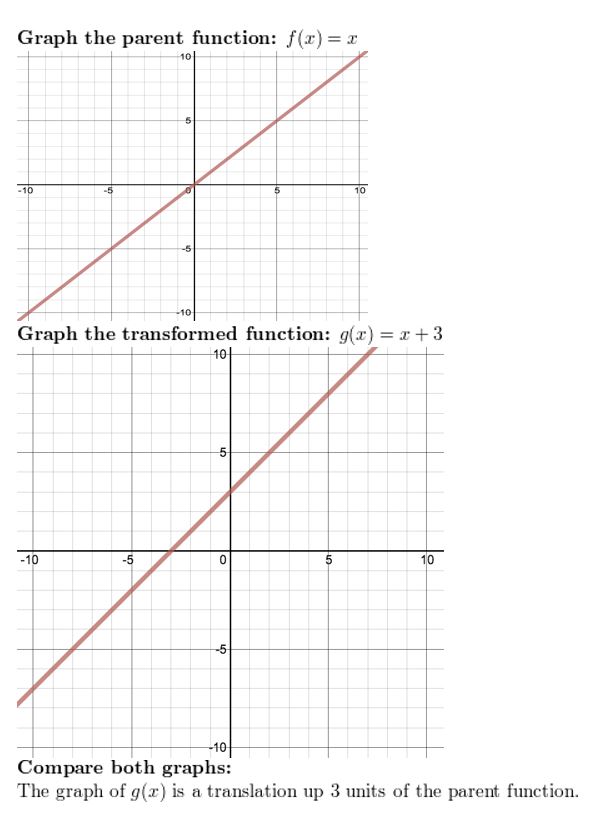
Question 3.
h(x) = (x – two)²

Question 4.
n(10) = – | x |

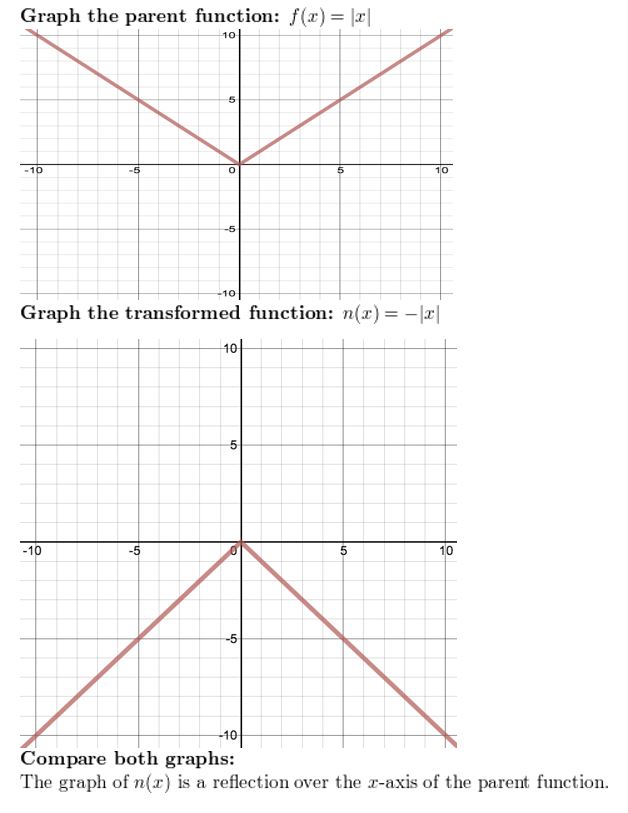
Graph the part and its parent function. So describe the transformation.

Question five.
thou(x) = 3x

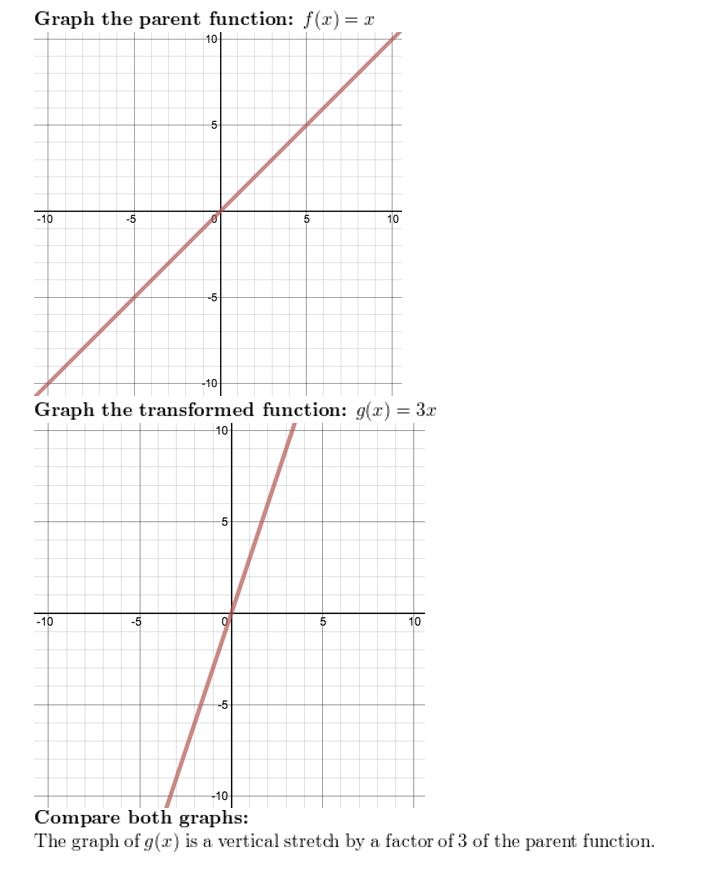
Question vi.
h(x) = \(\frac{3}{ii}\)x^two

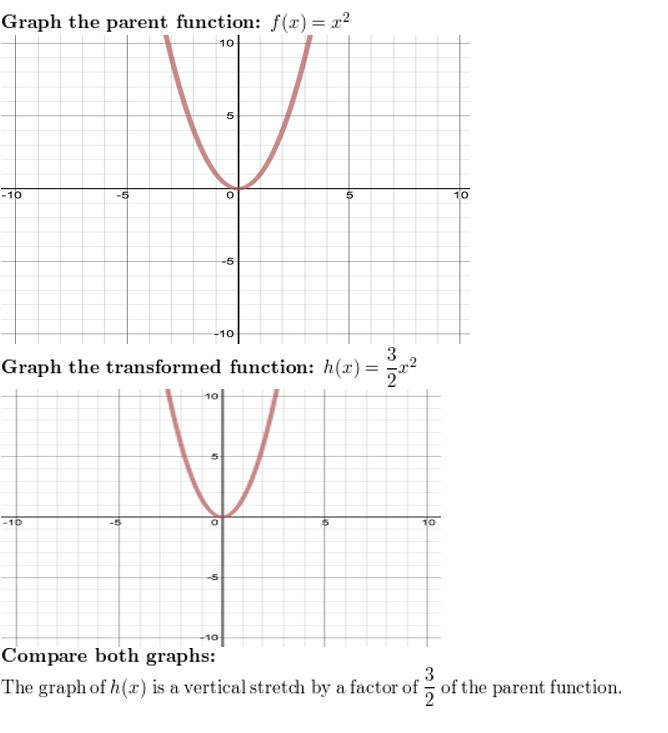
Question 7.
c(x) = 0.2|x|

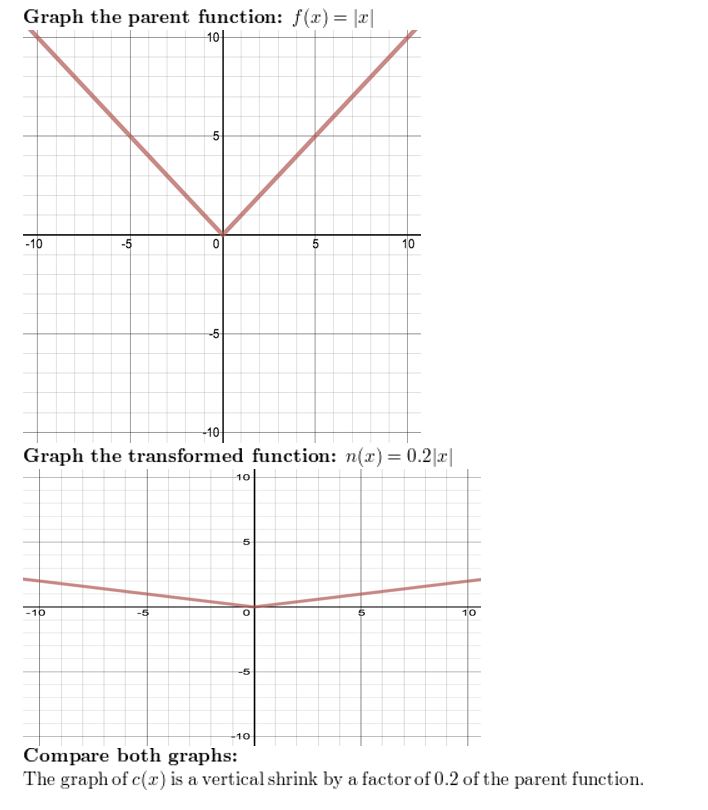
Apply a graphing calculator to graph the function and its parent function. And then describe the transformations

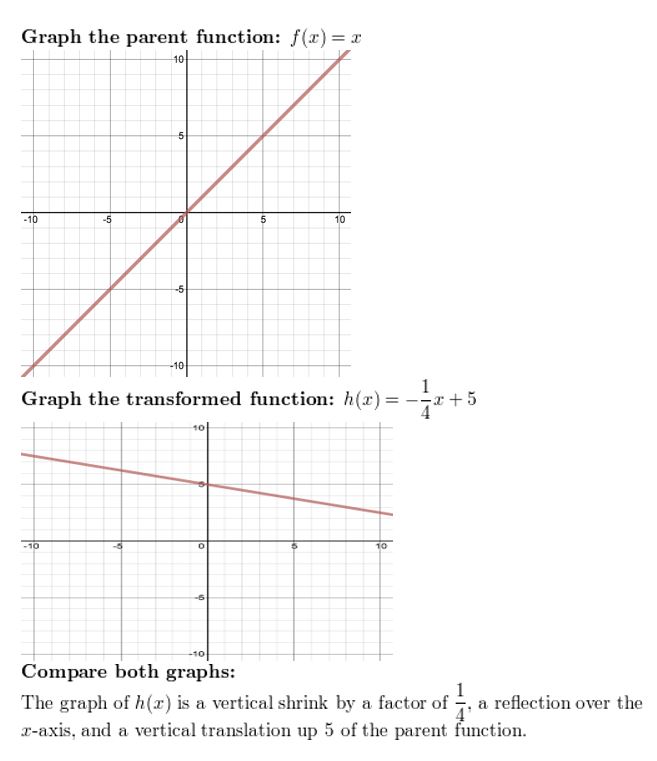
Question 8.
h(x) = –\(\frac{1}{4}\)10 + 5

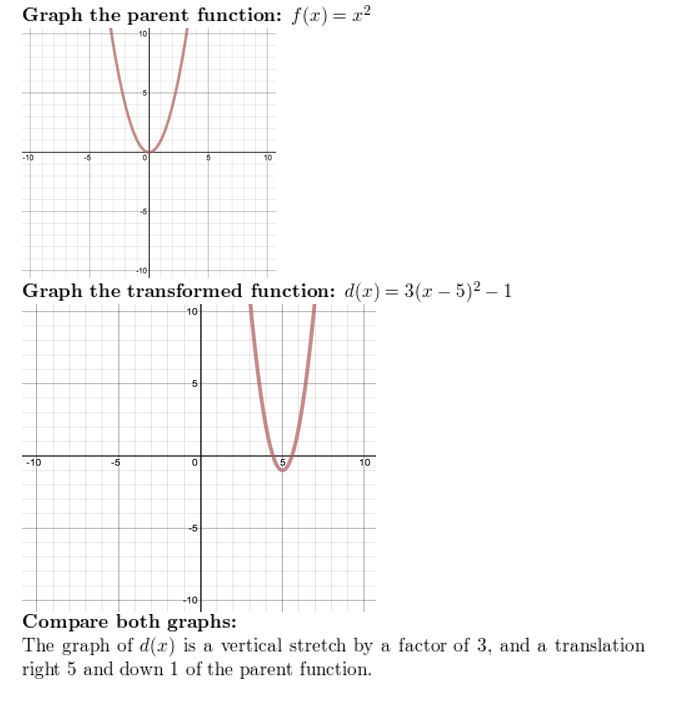
Question 9.
d(x) = 3(10 – five)² – 1

Question 10.
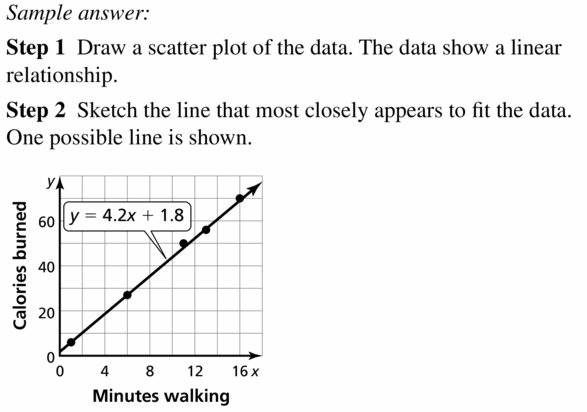
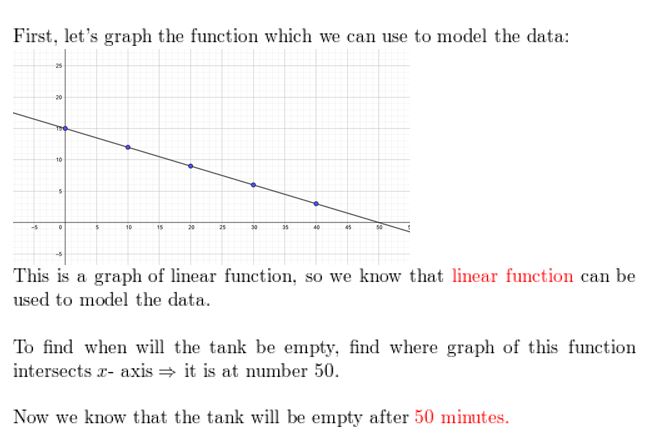
The table shows the amount of fuel in a chainsaw over time. What type of part can you use to model the data? When will the tank be empty?

Parent Functions and Transformations 1.1 Exercises

Vocabulary and Core Concept Check

Question 1.
Complete THE Sentence
The role f(x) = 10^two is the ______ of f(x) = 2x² – 3.
Respond:

Question 2.
DIFFERENT WORDS, SAME QUESTION Which is dissimilar? Find "both" answers.

Respond:

Monitoring Progress and Modeling with Mathematics

In Exercises 3–half-dozen, place the function family unit to which f belongs. Compare the graph of f to the graph of its parent part.

Question 3.

Answer:

Question 4.

Answer:

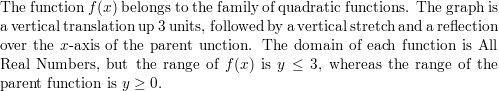
Question 5.

Respond:

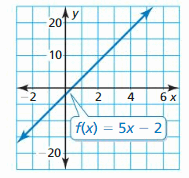
Question 6.

Answer:

Question 7.
MODELING WITH MATHEMATICS
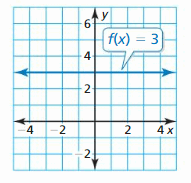
At viii:00 A.M., the temperature is 43°F. The temperature increases 2°F each hr for the next 7 hours. Graph the temperatures over time t (t = 0 represents 8:00 A.K.). What type of office can you apply to model the data? Explain.
Answer:

Question 8.
MODELING WITH MATHEMATICS
Y'all purchase a automobile from a dealership for $10,000. The trade-in value of the car each twelvemonth later the purchase is given past the function f(x) = 10,000 – 250x². What type of function models the trade-in value?
Reply:

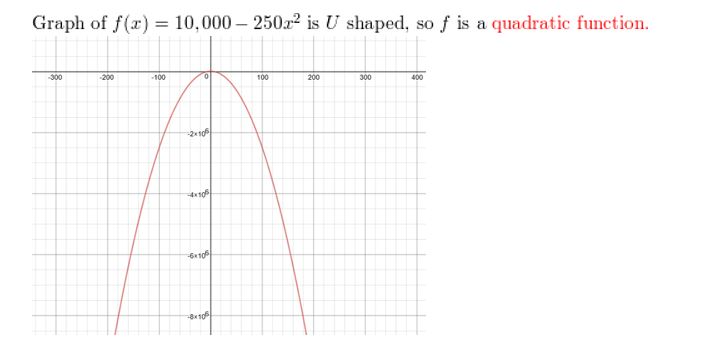
In Exercises ix–18, graph the function and its parent function. Then draw the transformation.

Question 9.
1000(x) = ten + iv
Answer:

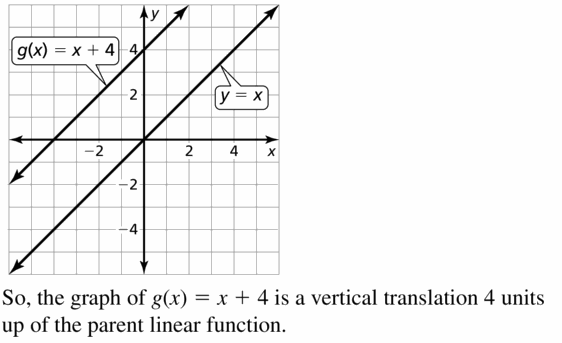
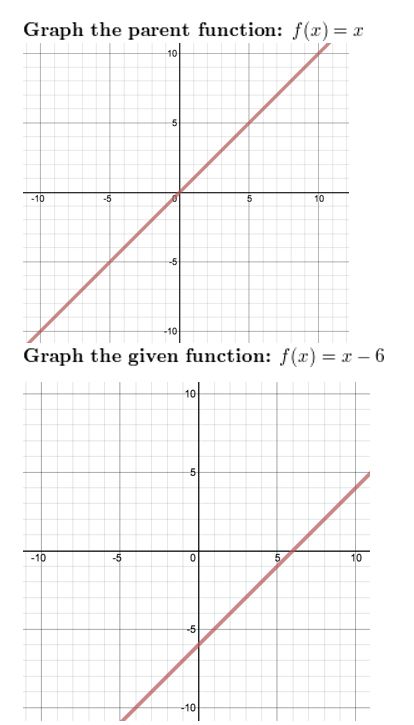
Question ten.
f(10) = x – 6
Answer:

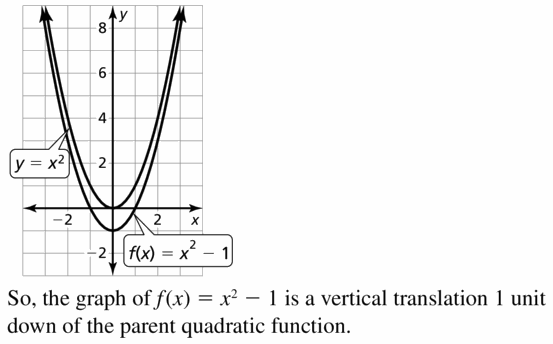
Question xi.
f(x) = x² – 1
Answer:

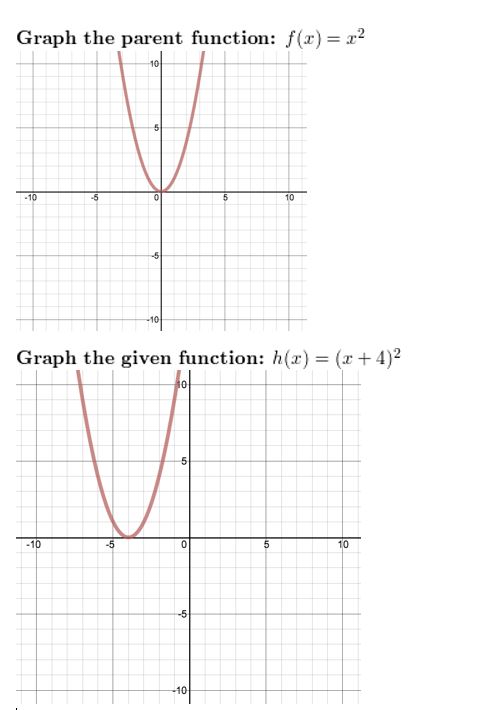
Question 12.
h(x) = (ten+ 4)^two
Answer:

Question 13.
grand(x) = | 10 – 5 |
Answer:

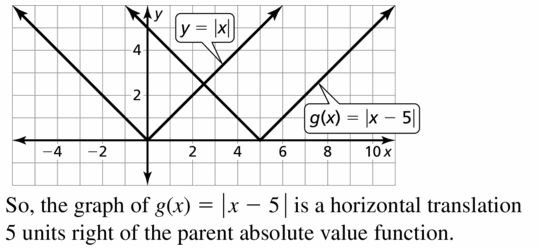
Question 14.
f(x) = 4 + | ten |
Reply:

Question 15.
h(x) = -x^two

Answer:

Question 16.
grand(x) = -x
Answer:

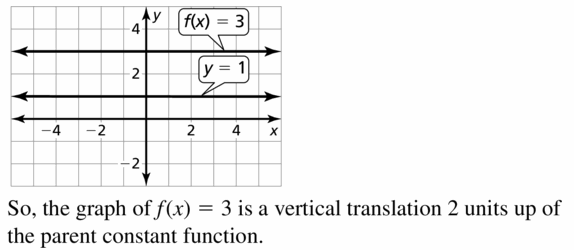
Question 17.
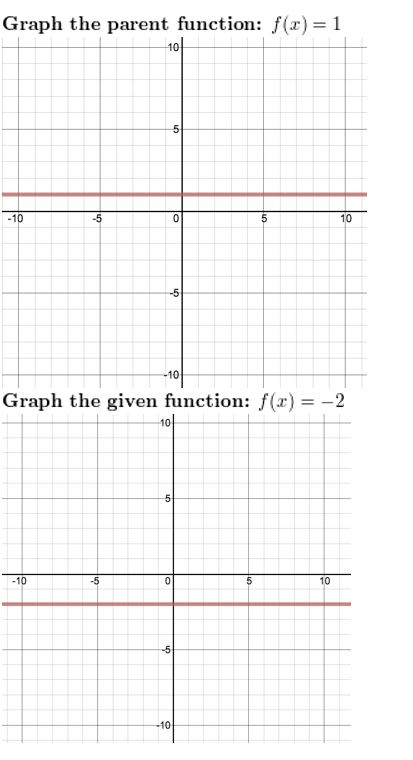
f(10) = 3
Respond:

Question eighteen.
f(x) = -2
Answer:

In Exercises xix–26, graph the part and its parent function. Then describe the transformation.

Question xix.
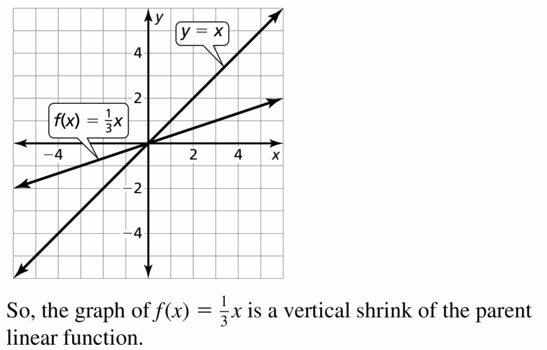
f(x) = \(\frac{1}{3}\)x
Answer:

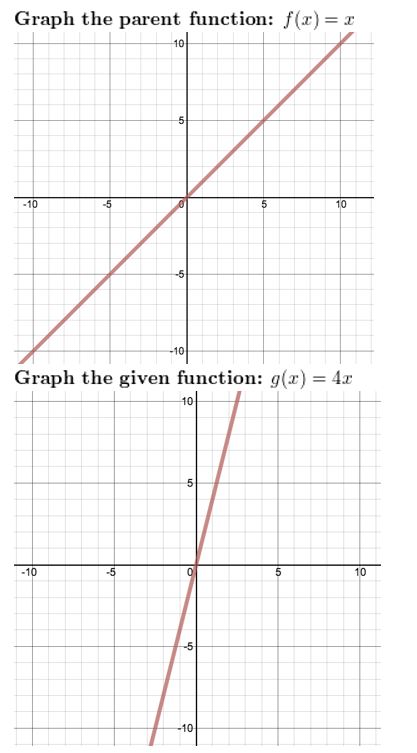
Question 20.
1000(x) = 4x
Answer:

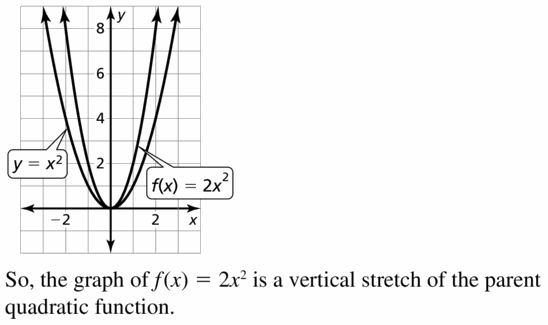
Question 21.
f(x) = 2xⁱⁱ

Answer:

Question 22.
h(x) = \(\frac{1}{three}\)x²

Answer:

Question 23.
h(10) = \(\frac{3}{four}\)x
Answer:

Question 24.
k(ten) = \(\frac{iv}{three}\)x
Answer:

Question 25.
h(ten) = iii | x |
Answer:

Question 26.
f(x) = \(\frac{1}{two}\) | x |
Reply:

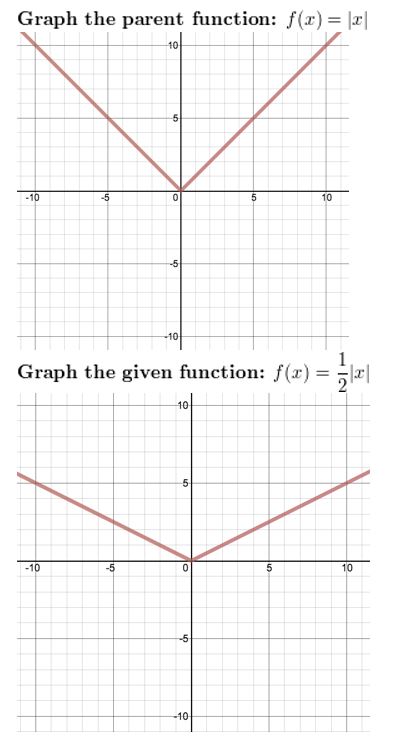
In Exercises 27–34, use a graphing calculator to graph the role and its parent function. Then draw the transformations.

Question 27.
f(x) = 3x + 2
Reply:

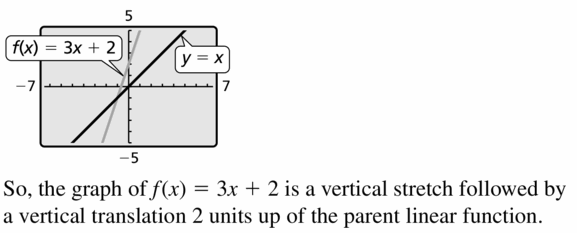
Question 28.
h(x) = -x + 5
Answer:

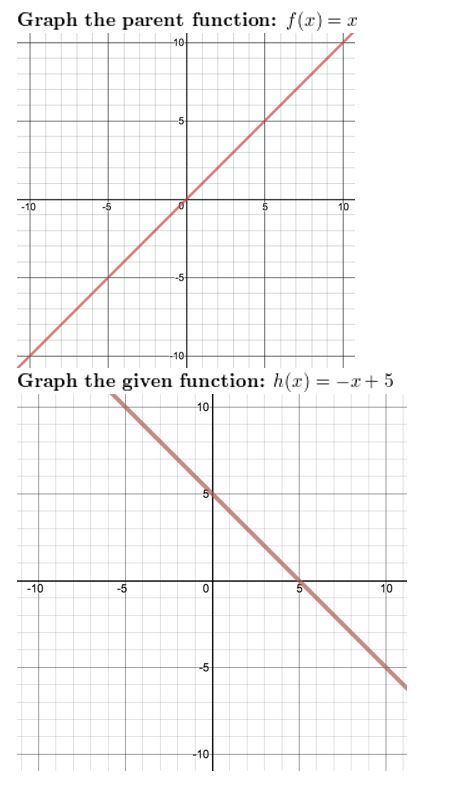
Question 29.
h(x) = -three | x | – 1
Answer:

Question 30.
f(x) = \(\frac{3}{4}\) | ten | + ane
Answer:

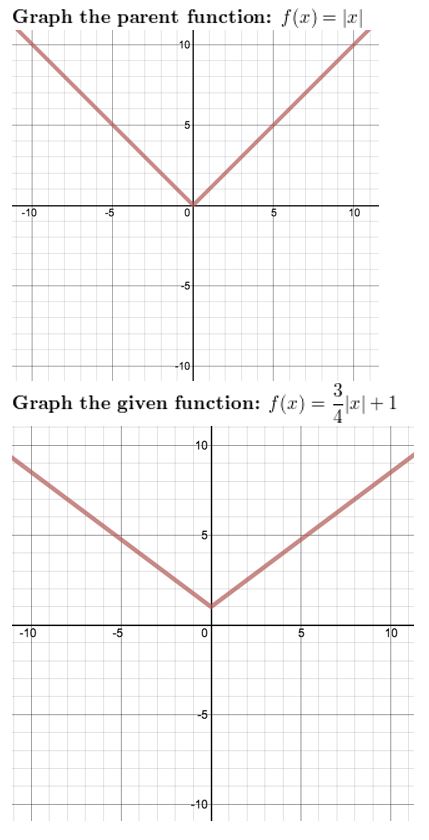
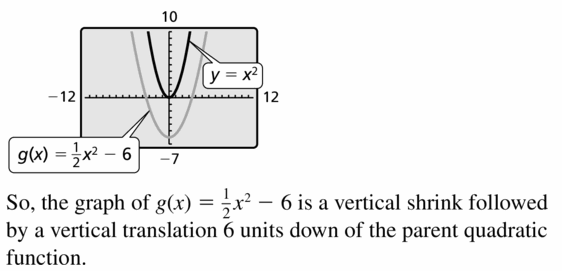
Question 31.
g(x) = \(\frac{1}{2}\)x² – 6
Reply:

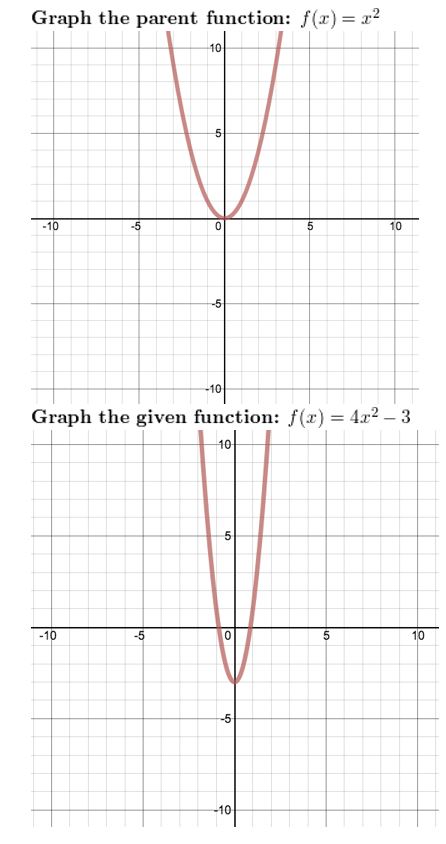
Question 32.
f(x) = 4x² – 3
Answer:

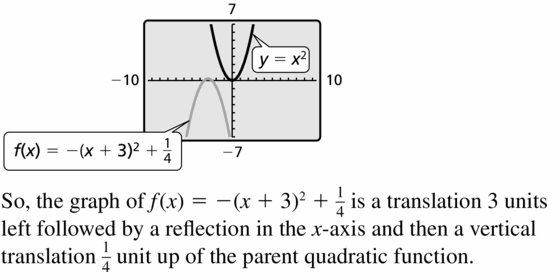
Question 33.
f(x) = -(x + 3)² + \(\frac{1}{iv}\)
Answer:

Question 34.
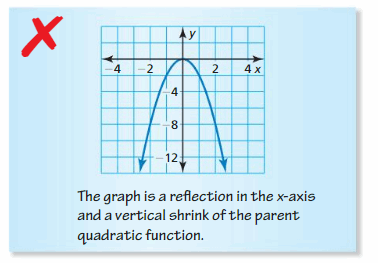
yard(x) = – | x – 1 | – \(\frac{one}{2}\)
Respond:

ERROR Assay In Exercises 35 and 36, place and correct the error in describing the transformation of the parent role.

Question 35.

Answer:

Question 36.

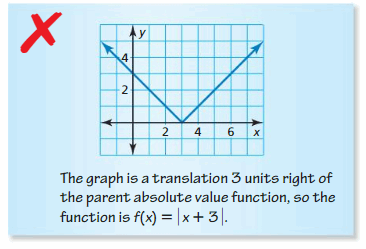
Answer:

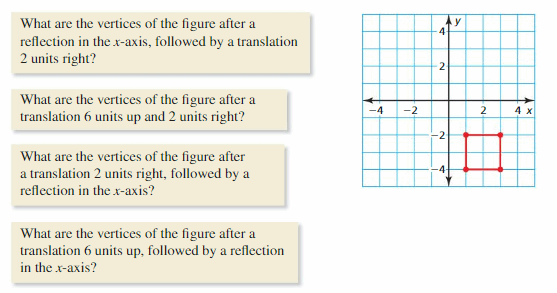
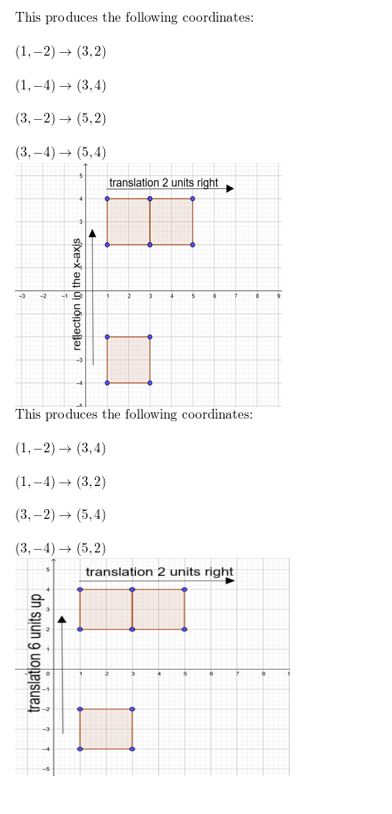
MATHEMATICAL CONNECTIONS In Exercises 37 and 38, find the coordinates of the figure after the transformation.

Question 37.
Translate 2 units down.

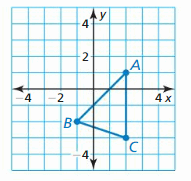
Answer:

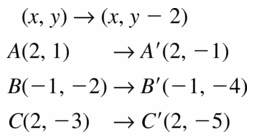
Question 38.
Reflect in the 10-centrality.

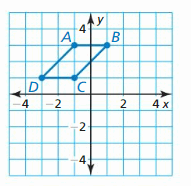
Answer:

USING TOOLS In Exercises 39–44, identify the office family and describe the domain and range. Use a graphing calculator to verify your answer.

Question 39.
1000(x) = | ten + 2 | – 1
Answer:

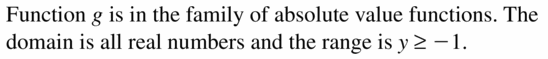
Question 40.
h(ten) = | x – 3 | + 2
Answer:

Question 41.
chiliad(x) = 3x + 4
Reply:

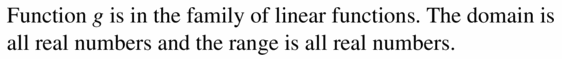
Question 42.
f(x) = -4x + 11
Answer:

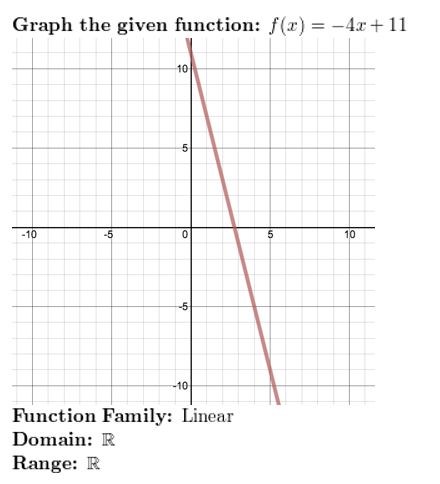
Question 43.
f(x) = 5x^two – 2
Answer:

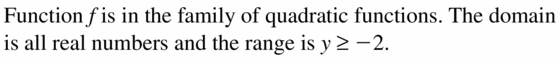
Question 44.
f(x) = -2x² + 6
Answer:

Question 45.
MODELING WITH MATHEMATICS The table shows the speeds of a car as it travels through an intersection with a stop sign. What type of part tin can yous use to model the data? Estimate the speed of the machine when information technology is 20 yards past the intersection.

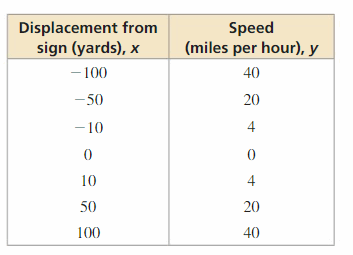
Answer:

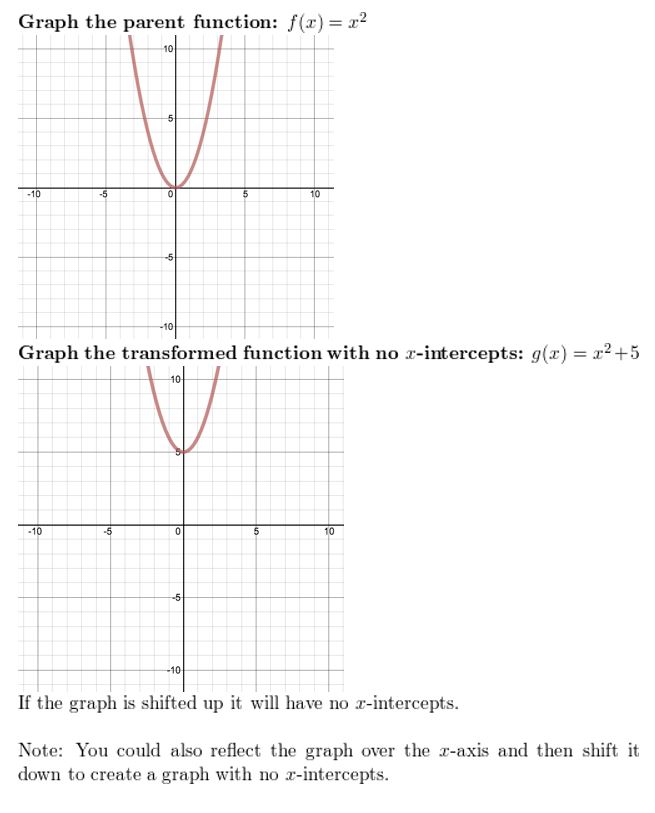
Question 46.
Idea PROVOKING In the same coordinate plane, sketch the graph of the parent quadratic role and the graph of a quadratic function that has no x-intercepts. Describe the transformation(south) of the parent role.
Reply:

Question 47.
USING Structure Graph the functions f(x) = | 10 – 4 | and one thousand(10) = | x | – 4. Are they equivalent? Explain.
Reply:

Question 48.
HOW Practice Yous SEE Information technology? Consider the graphs of f, g, and h.

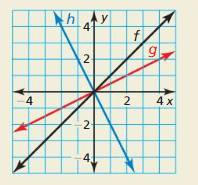
a. Does the graph of g correspond a vertical stretch or a vertical shrink of the graph of f? Explain your reasoning.
b. Describe how to transform the graph of f to obtain the graph of h.
Answer:

Question 49.
MAKING AN ARGUMENT Your friend says ii different translations of the graph of the parent linear part can result in the graph of f(x) = ten – ii. Is your friend correct? Explain.
Answer:

Question 50.
Drawing CONCLUSIONS A person swims at a abiding speed of one meter per 2d. What type of function can be used to model the distance the swimmer travels? If the person has a ten-meter head start, what type of transformation does this stand for? Explain.

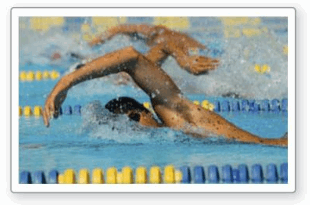
Reply:

Question 51.
PROBLEM SOLVING You are playing basketball with your friends. The tiptop (in anxiety) of the ball above the ground t seconds after a shot is released from your hand is modeled by the office f(t) = -16t² + 32t + five.two.
a. Without graphing, identify the type of function that models the height of the basketball.
b. What is the value of t when the ball is released from your hand? Explicate your reasoning.
c. How many anxiety in a higher place the ground is the ball when it is released from your mitt? Explain.
Answer:

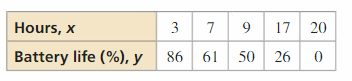
Question 52.
MODELING WITH MATHEMATICS The tabular array shows the battery lives of a computer over time. What type of office tin can y'all use to model the data? Interpret the pregnant of the 10-intercept in this situation.

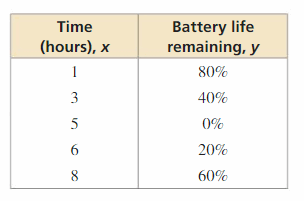
Answer:

Question 53.
REASONING Compare each function with its parent office. State whether it contains a horizontal translation, vertical translation, both, or neither. Explain your reasoning.
a. f(10) = two | 10 | – 3
b. f(x) = (x – 8)²
c. f(x) = | ten + 2 | + 4
d. f(x) = 4x²

Answer:

Question 54.
Disquisitional THINKING
Apply the values -1, 0, 1, and 2 in the correct box so the graph of each part intersects the ten-axis. Explain your reasoning.

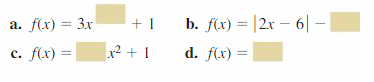
Answer:

Maintaining Mathematical Proficiency

Determine whether the ordered pair is a solution of the equation. (Skills Review Handbook)

Question 55.
f(x) = | x + 2 |; (ane, -three)
Answer:

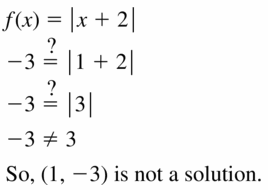
Question 56.
f(10) = | x | – 3; (-2, -5)
Answer:

Question 57.
f(10) = x – three; (five, two)
Answer:

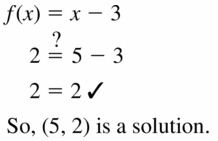
Question 58.
f(x) = x – 4; (12, 8)
Answer:

Find the 10-intercept and the y-intercept of the graph of the equation. (Skills Review Handbook)

Question 59.
y = x
Answer:

Question 60.
y = 10 + 2
Reply:

Question 61.
3x + y = 1
Reply:

Question 62.
x – 2y = 8
Reply:

Lesson 1.2 Transformations of Linear and Absolute Value Functions

Essential Question

How do the graphs of y = f(x) + k, y = f(x – h), and y = -f(10) compare to the graph of the parent function f?

EXPLORATION ane
Transformations of the Parent Absolute Value Function
Work with a partner. Compare the graph of the role

y = | x | + 1000 Transformation

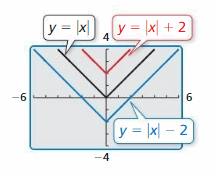
to the graph of the parent part
f(10) = | 10 |.

EXPLORATION two
Transformations of the Parent Absolute Value Function
Work with a partner. Compare the graph of the role
y = | x – h | Transformation
to the graph of the parent role
f(x) = | x |. Parent function

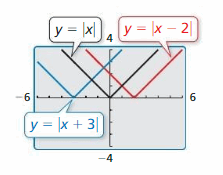
EXPLORATION 3
Transformation of the Parent Absolute Value Part
Work with a partner. Compare the graph of the function
y = – | 10 | Transformation
to the graph of the parent function
f(x) = | x | Parent function

Communicate Your Answer

Question 4.
Transformation How do the graphs of y = f (x) + m, y = f(x – h), and y = -f(x) compare to the graph of the parent role f?

Question v.
Compare the graph of each function to the graph of its parent role f. Use a graphing estimator to verify your answers are correct.
a. y = \([\sqrt{x}/latex] – iv
b. y = [latex][\sqrt{x + 4}/latex]
c. y = –[latex][\sqrt{ten}/latex]
d. y = x² + 1
east. y = (x – 1)^two
f. y = -ten²

one.2 Lesson

Monitoring Progress

Write a function 1000 whose graph represents the indicated transformation of the graph of f. Use a graphing calculator to cheque your answer.

Question 1.
f(x) = 3x; translation 5 units up

Question two.
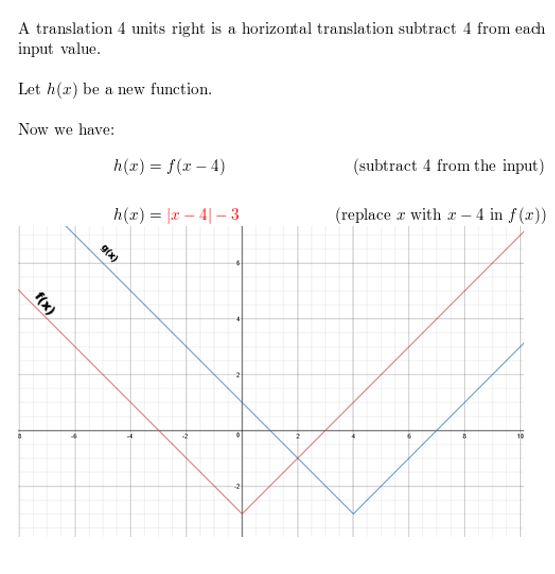
f(10) = | x | – 3; translation iv units to the correct

Question three.
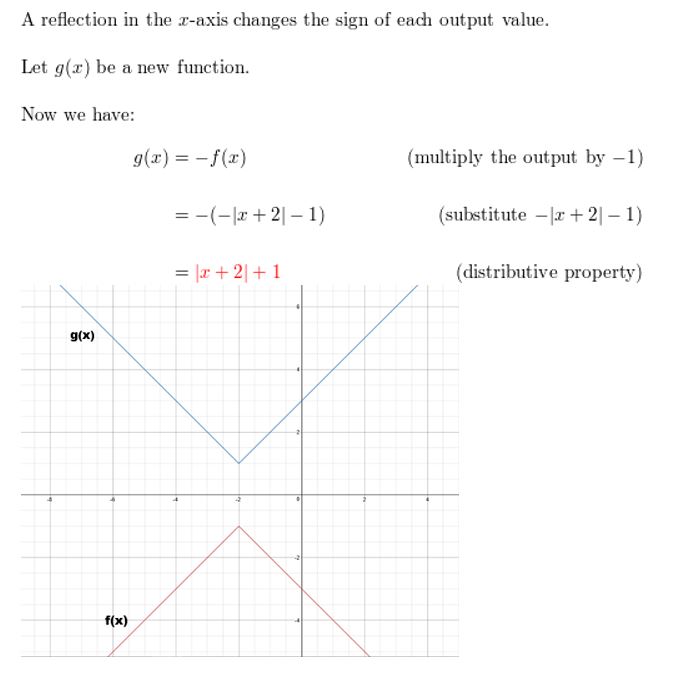
f(x) = – | ten + 2 | – 1; reflection in the 10-centrality

Question 4.
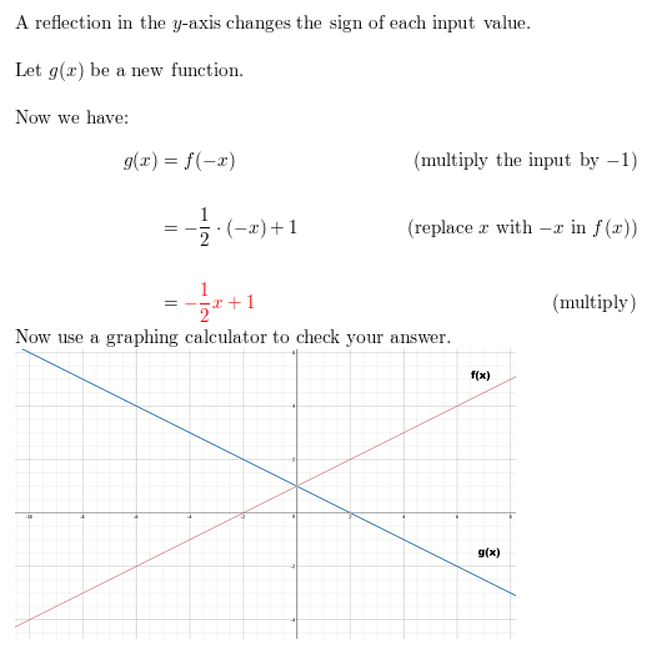
f(x) = [latex]\frac{1}{2}\)x+ i; reflection in the y-axis

Write a role g whose graph represents the indicated transformation of the graph of f. Utilize a graphing figurer to check your answer.

Question 5.
f(ten) = 4x+ 2; horizontal stretch past a gene of ii

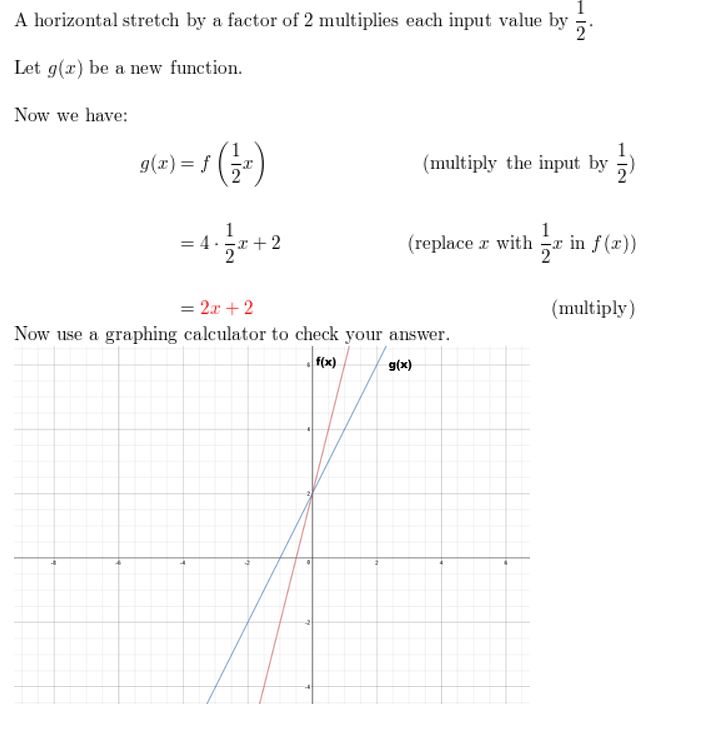
Question 6.
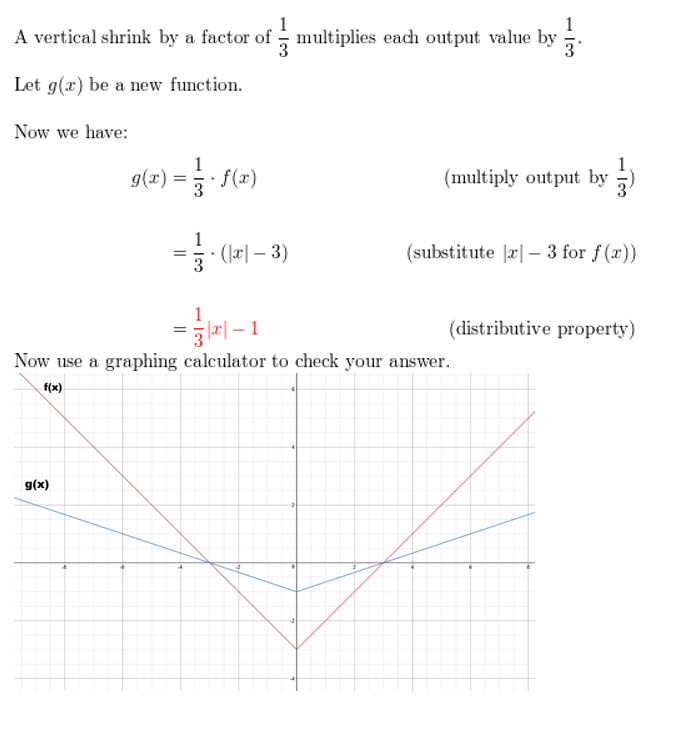
f(10) = | x | – three; vertical shrink by a factor of \(\frac{1}{three}\)

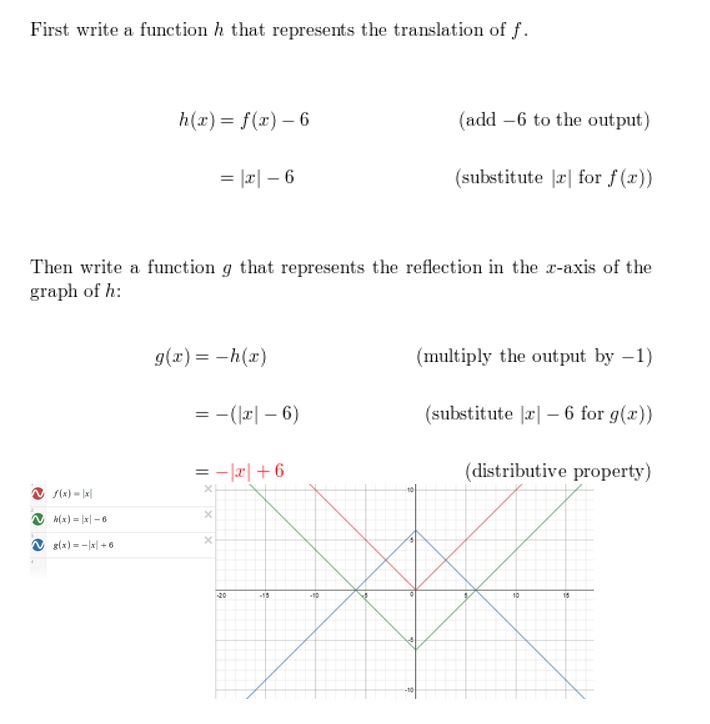
Question 7.
Permit the graph of m be a translation 6 units downwardly followed by a reflection in the x-axis of the graph of f(10) = | x |. Write a rule for g. Use a graphing estimator to cheque your answer.

Question 8.
WHAT IF? In Example 5, your revenue function is f(x) = 3x. How does this affect your profit for 100 downloads?

Transformations of Linear and Absolute Value Functions 1.2 Exercises

Vocabulary and Cadre Concept Bank check

Question ane.
Consummate THE SENTENCE
The function g(10) = | 5x |- 4 is a horizontal ___________ of the part f(x) = | x | – 4.
Answer:

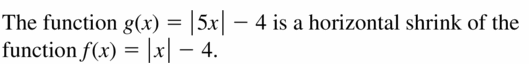
Question 2.
WHICH 1 DOESN'T Vest? Which transformation does not belong with the other 3? Explain your reasoning.

Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3–eight, write a office g whose graph represents the indicated transformation of the graph of f. Employ a graphing calculator to check your answer.

Question 3.
f(x) = x – 5; translation 4 units to the left
Respond:

Question 4.
f(x) = ten + 2; translation 2 units to the right
Answer:

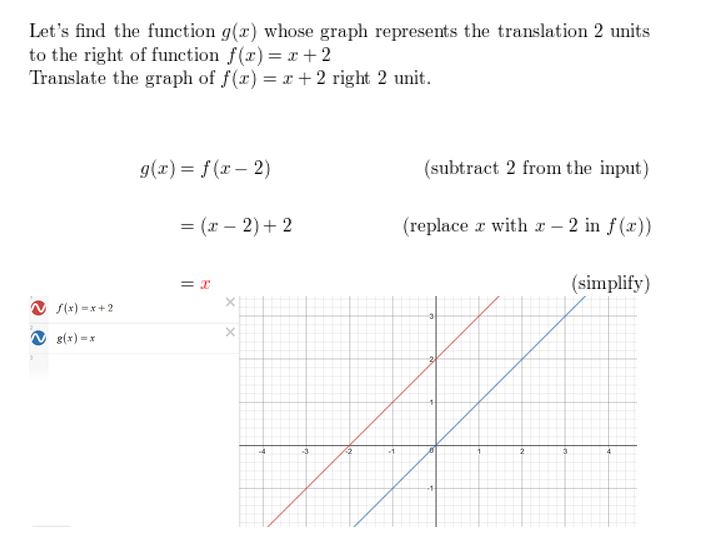
Question 5.
f(x) = | 4x + 3 | + ii; translation 2 units down
Answer:

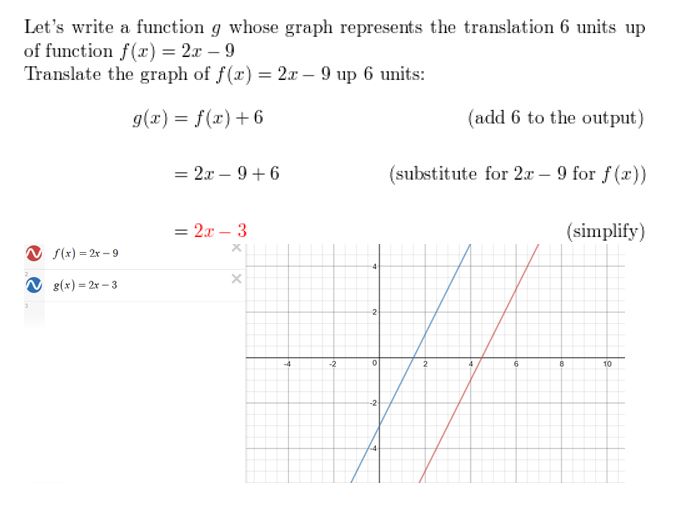
Question 6.
f(x) = 2x – 9; translation 6 units up
Reply:

Question 7.
f(x) = 4 – | x + 1 |

Answer:

Question 8.
f(10) = | 4x | + 5

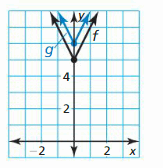
Answer:

Question 9.
WRITING Describe two dissimilar translations of the graph of f that result in the graph of thou.

Answer:

Question 10.
Trouble SOLVING You open a café. The part f(x) = 4000x represents your expected net income (in dollars) after beingness open x weeks. Earlier you open, you incur an extra expense of $12,000. What transformation of f is necessary to model this state of affairs? How many weeks will it take to pay off the extra expense?

Answer:

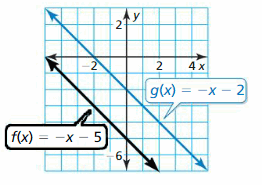
In Exercises 11–16, write a function g whose graph represents the indicated transformation of the graph of f. Utilise a graphing calculator to check your reply.

Question eleven.
f(x) = -5x+ 2; reflection in the x-axis
Answer:

Question 12.
f(x) = \(\frac{1}{two}\)x – 3; reflection in the 10-centrality
Answer:

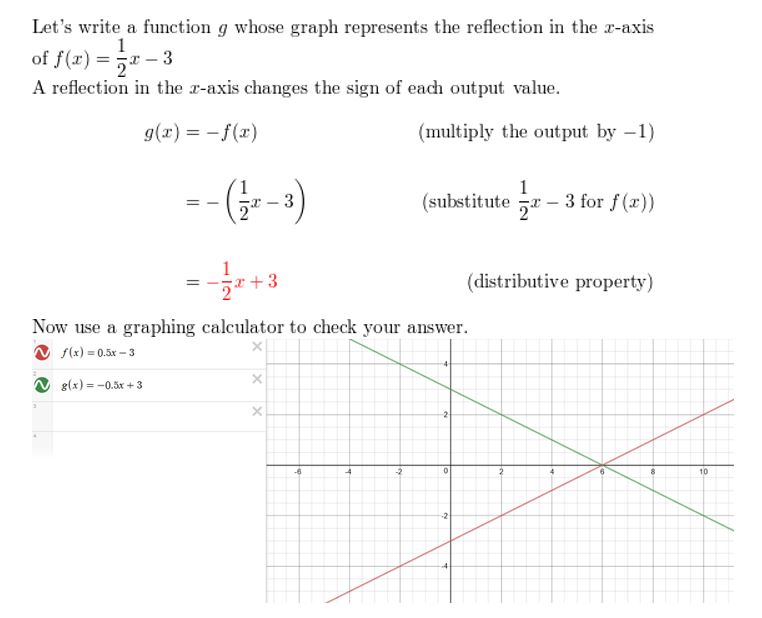
Question thirteen.
f(10) = | 6x | – 2; reflection in the y-axis
Reply:

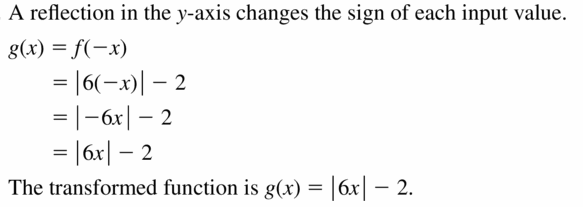
Question 14.
f(x) = | 2x – one | + 3; reflection in the y-centrality
Respond:

Question 15.
f(ten) = -3 + | x – 11 |; reflection in the y-axis
Answer:

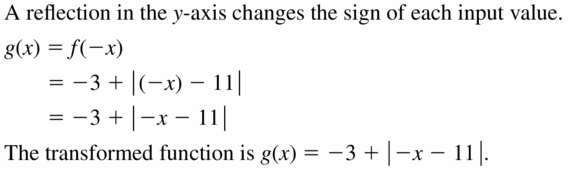
Question 16.
f(ten) = -x+ 1; reflection in the y-axis

In Exercises 17–22, write a function g whose graph represents the indicated transformation of the graph of f. Use a graphing calculator to check your answer.

Question 17.
f(10) = x + two; vertical stretch by a factor of five
Answer:

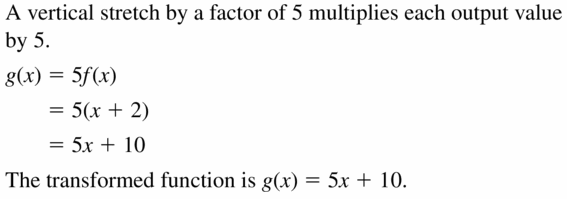
Question xviii.
f(x) = 2x+ 6; vertical shrink by a cistron of \(\frac{1}{two}\)
Answer:

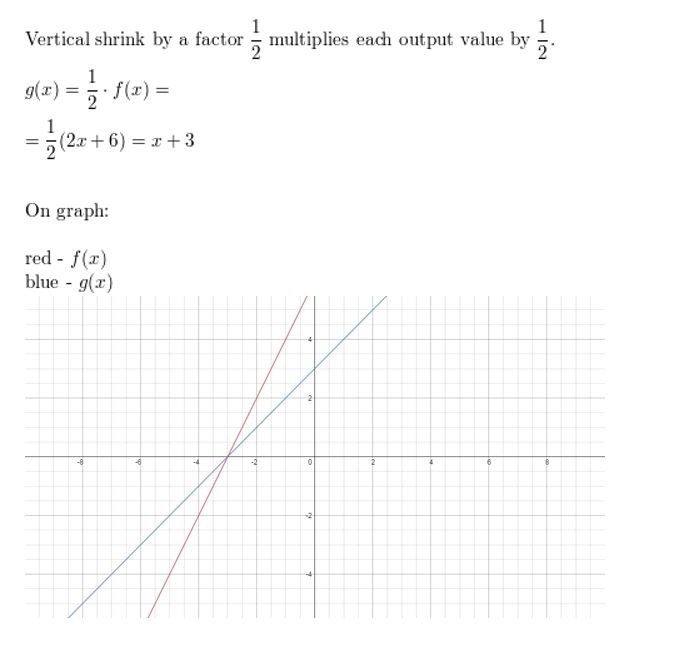
Question 19.
f(x) = | 2x | + iv; horizontal compress past a factor of \(\frac{1}{two}\)
Reply:

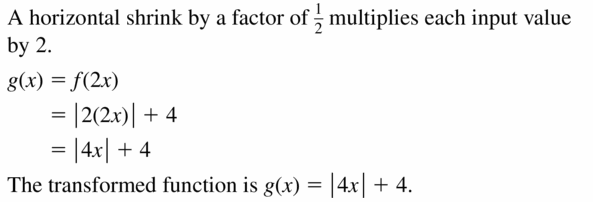
Question 20.
f(x) = | x+ iii | ; horizontal stretch past a factor of 4
Answer:

Question 21.
f(x) = -2 | x – 4 | + two

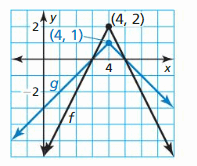
Answer:

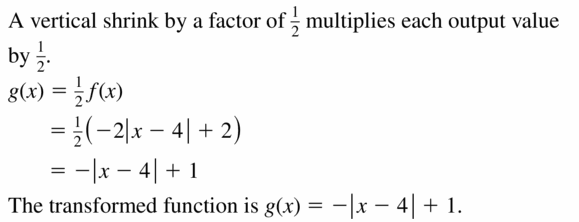
Question 22.
f(x) = 6 – 10

Reply:

ANALYZING RELATIONSHIPS In Exercises 23–26, match the graph of the transformation of f with the correct equation shown. Explicate your reasoning.

Question 23.

Answer:

Question 24.

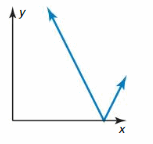
Respond:

Question 25.

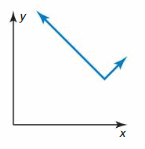
Answer:

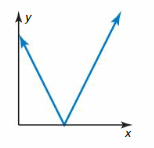
Question 26.

Answer:
A. y = 2f(x)
B. y = f(2x)
C. y = f(x + ii)
D. y = f(x) + 2

In Exercises 27–32, write a part m whose graph represents the indicated transformations of the graph of f.

Question 27.
f(10) = x; vertical stretch by a factor of 2 followed by a translation i unit upwards
Answer:

Question 28.
f(x) = x; translation 3 units downwardly followed by a vertical shrink by a factor of \(\frac{1}{iii}\)
Answer:

Question 29.
f(x) = | x | ; translation two units to the right followed past a horizontal stretch by a factor of two
Reply:

Question 30.
f(x) = | x |; reflection in the y-axis followed by a translation 3 units to the right
Answer:

Question 31.
f(ten) = | x |

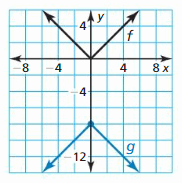
Answer:

Question 32.
f(10) = | 10 |

Reply:

Fault ANALYSIS In Exercises 33 and 34, identify and correct the fault in writing the function k whose graph represents the indicated transformations of the graph of f.

Question 33.

Answer:

Question 34.

Answer:

Question 35.
MAKING AN ARGUMENT Your friend claims that when writing a function whose graph represents a combination of transformations, the order is not of import. Is your friend right? Justify your answer.
Answer:

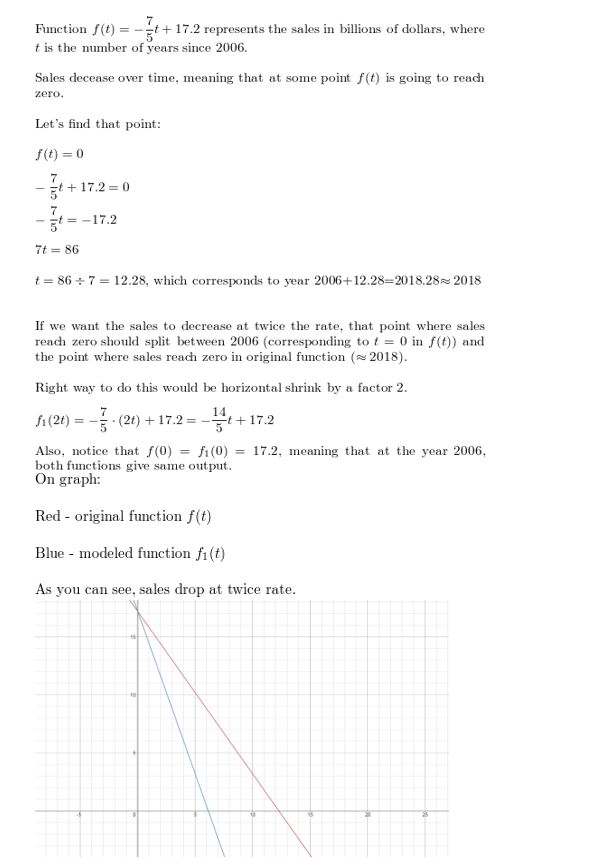
Question 36.
MODELING WITH MATHEMATICS During a recent period of fourth dimension, bookstore sales have been declining. The sales (in billions of dollars) tin be modeled by the function f(t) = –\(\frac{7}{five}\)t + 17.2, where t is the number of years since 2006. Suppose sales decreased at twice the rate. How tin you transform the graph of f to model the sales? Explicate how the sales in 2010 are afflicted by this change.
Answer:

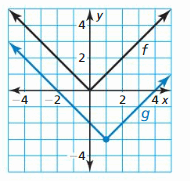
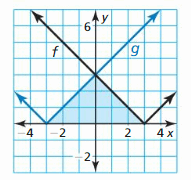
MATHEMATICAL CONNECTIONS For Exercises 37–40, describe the transformation of the graph of f to the graph of g. Then detect the area of the shaded triangle.

Question 37.
f(ten) = | x – three |

Answer:

Question 38.
f(10) = – | x | – two

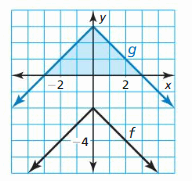
Answer:

Question 39.
f(x) = -x + 4

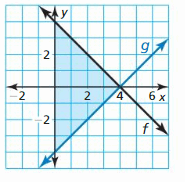
Answer:

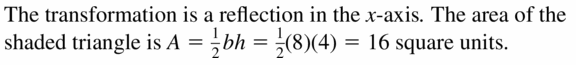
Question twoscore.
f(10) = x – 5

Answer:

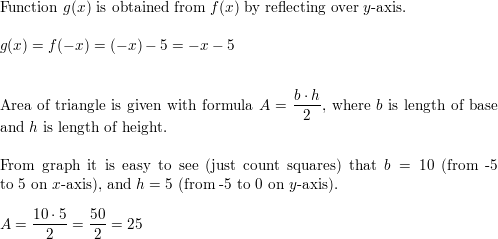
Question 41.
Abstruse REASONING The functions f(x) = mx + b and g(x) = mx + c represent two parallel lines.
a. Write an expression for the vertical translation of the graph of f to the graph of g.
b. Use the definition of slope to write an expression for the horizontal translation of the graph of f to the graph of grand.
Answer:

Question 42.
HOW DO You Meet IT? Consider the graph of f(ten) = mx + b. Describe the outcome each transformation has on the gradient of the line and the intercepts of the graph.

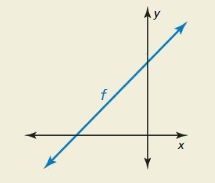
a. Reflect the graph of f in the y-axis.
b. Compress the graph of f vertically by a factor of \(\frac{i}{3}\).
c. Stretch the graph of f horizontally by a factor of 2.
Answer:

Question 43.
REASONING The graph of thousand(x) = -4 |x | + two is a reflection in the x-axis, vertical stretch by a factor of 4, and a translation 2 units down of the graph of its parent office. Choose the correct order for the transformations of the graph of the parent function to obtain the graph of m. Explain your reasoning.
Answer:

Question 44.
THOUGHT PROVOKING Y'all are planning a cross-country bicycle trip of 4320 miles. Your altitude d (in miles) from the halfway point can be modeled by d = 72 |x – 30 |, where x is the time (in days) and x = 0 represents June 1. Your plans are altered so that the model is now a right shift of the original model. Give an example of how this tin happen. Sketch both the original model and the shifted model.
Answer:

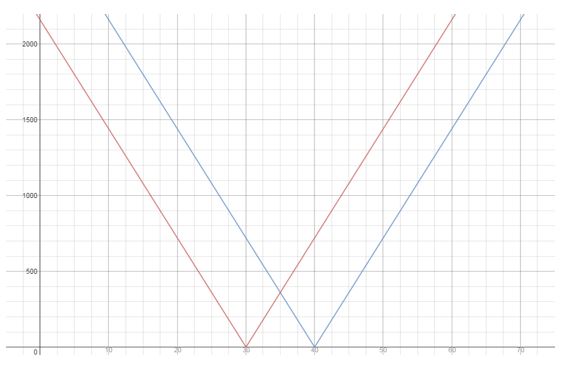
Question 45.
Critical THINKING Use the right value 0, -2, or 1 with a, b, and c then the graph of k(x) = a|10 – b | + c is a reflection in the x-axis followed past a translation ane unit to the left and one unit up of the graph of f(x) = 2 |10 – two | + 1. Explain your reasoning.
Answer:

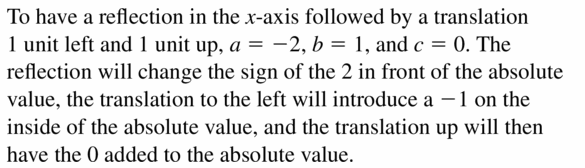
Maintaining Mathematical Proficiency

Evaluate the office for the given value of ten. (Skills Review Handbook)

Question 46.
f(x) = x + iv; 10 = three
Respond:

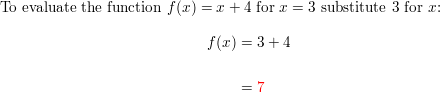
Question 47.
f(x) = 4x – ane; x = -one
Answer:

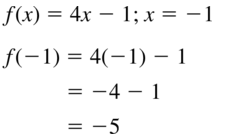
Question 48.
f(x) = -x + 3; ten = five
Answer:

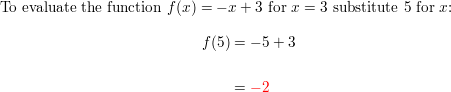
Question 49.
f(10) = -2x – 2; x = -1
Answer:

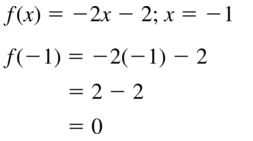
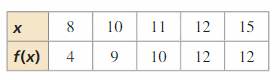
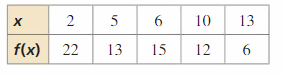
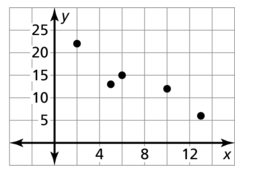
Create a scatter plot of the information. (Skills Review Handbook)

Question 50.

Answer:

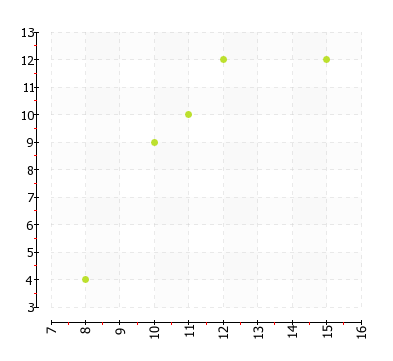
Question 51.

Answer:

Linear Functions Study Skills Taking Control of Your Class Time

ane.one – 1.2 What Did You lot Learn?

Core Vocabulary

Cadre Concepts

Section 1.one

Section one.2

Mathematical Practices

Question 1.
How tin y'all clarify the values given in the tabular array in Practise 45 on page 9 to aid you decide what blazon of part models the data?

Question 2.
Explicate how you would circular your respond in Exercise 10 on page 16 if the extra expense is $13,500.

Written report Skills

Taking Command of Your Class Time

Question one.
Sit down where y'all can hands run across and hear the teacher, and the teacher can see y'all.

Question 2.
Pay attention to what the instructor says nearly math, not merely what is written on the board.

Question 3.
Ask a question if the teacher is moving through the textile likewise fast.

Question four.
Try to memorize new information while learning it.

Question v.
Enquire for clarification if you lot do not empathize something.

Question 6.
Remember as intensely equally if you were going to take a quiz on the material at the end of course.

Question 7.
Volunteer when the teacher asks for someone to go upward to the lath.

Question eight.
At the finish of class, place concepts or problems for which you still need clarification.

Question 9.
Use the tutorials at BigIdeasMath.com for boosted assistance.

Linear Functions 1.1-1.2 Quiz

Identify the office family to which thousand belongs. Compare the graph of the office to the graph of its parent part. (Section 1.1)

Question 1.

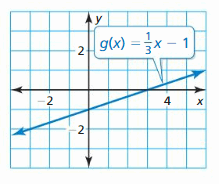
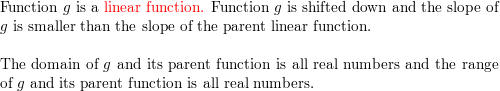
Question 2.

Question three.

Graph the office and its parent function. Then describe the transformation. (Section 1.1)

Question 4.
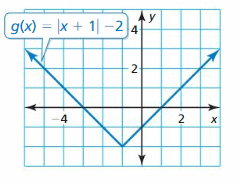
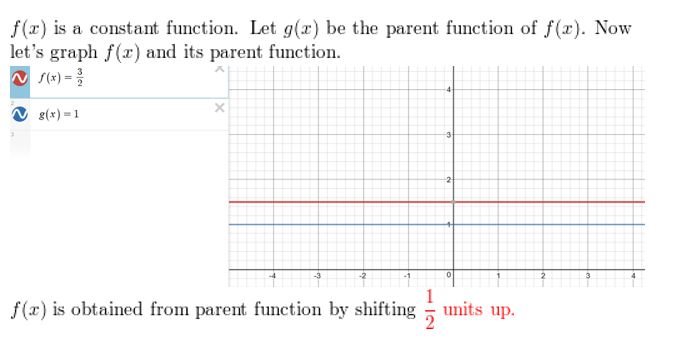
f(10) = \(\frac{3}{2}\)

Question 5.
f(x) = 3x

Question vi.
f(ten) = 2(x – 1)ⁱⁱ

Question 7.
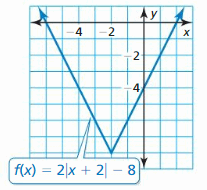
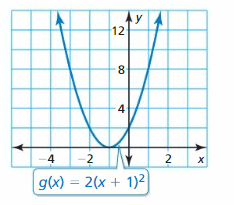
f(x) = – | x + 2 | – 7

Question 8.
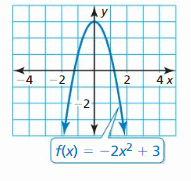
f(x) = \(\frac{one}{4}\)xⁱⁱ + one

Question 9.
f(x) = –\(\frac{one}{two}\)x – four

Write a function 1000 whose graph represents the indicated transformation of the graph of f. (Department one.2)

Question 10.
f(x) = 2x + i; translation 3 units up

Question 11.
f(x) = -3 | x – 4 | ; vertical shrink by a factor of \(\frac{1}{2}\)

Question 12.
f(x) = 3 | 10 + 5 |; reflection in the x-axis

Question 13.
f(x) = \(\frac{1}{3}\)ten – \(\frac{2}{three}\) ; translation four units left

Write a function g whose graph represents the indicated transformations of the graph of f. (Section 1.2)

Question fourteen.
Let g exist a translation 2 units down and a horizontal shrink by a factor of \(\frac{2}{3}\) of the graph of f(10) =ten.

Question 15.
Let 1000 exist a translation 9 units downwards followed by a reflection in the y-axis of the graph of f(x) = 10.

Question sixteen.
Allow g be a reflection in the x-centrality and a vertical stretch by a gene of 4 followed by a translation 7 units down and 1 unit right of the graph of f(ten) = | x |.

Question 17.
Let thousand be a translation 1 unit of measurement down and two units left followed by a vertical shrink by a factor of \(\frac{one}{2}\) of the graph of f(x) = | x |.

Question eighteen.
The table shows the total distance a new auto travels each month later on it is purchased. What type of function can you utilise to model the data? Estimate the mileage after i year. (Section i.1)

Question 19.
The total cost of an annual laissez passer plus camping for x days in a National Park tin can be modeled by the function f(ten) = 20x+ 80. Senior citizens pay half of this price and receive an additional $30 discount. Describe how to transform the graph of f to model the total cost for a senior citizen. What is the total cost for a senior citizen to go camping for three days? (Section one.ii)

Lesson 1.three Modeling with Linear Functions

Essential Question
How can you use a linear role to model and clarify a real-life situation?

EXPLORATION 1
Modeling with a Linear Part
Piece of work with a partner. A visitor purchases a copier for $12,000. The spreadsheet shows how the copier depreciates over an 8-year menses.
a. Write a linear function to stand for the value V of the copier equally a function of the number t of years.
b. Sketch a graph of the function. Explain why this blazon of depreciation is called straight line depreciation.
c. Interpret the slope of the graph in the context of the trouble.

EXPLORATION 2
Modeling with Linear Functions

Work with a partner. Match each description of the situation with its respective graph. Explain your reasoning.
a. A person gives $twenty per calendar week to a friend to repay a $200 loan.
b. An employee receives $12.50 per hour plus $2 for each unit produced per hour.
c. A sales representative receives $30 per day for food plus $0.565 for each mile driven.
d. A figurer that was purchased for $750 depreciates $100 per twelvemonth.

Communicate Your Answer

Question 3.
How tin you utilize a linear office to model and analyze a real-life situation?

Question iv.
Utilise the Internet or some other reference to find a real-life example of straight line depreciation.
a. Apply a spreadsheet to prove the depreciation.
b. Write a role that models the depreciation.
c. Sketch a graph of the role.

1.3 Lesson

Monitoring Progress

Question 1.
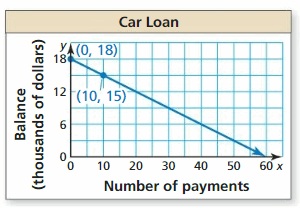
The graph shows the remaining balance y on a car loan afterwards making 10 monthly payments. Write an equation of the line and translate the gradient and y-intercept. What is the remaining residuum later 36 payments?

Question 2.
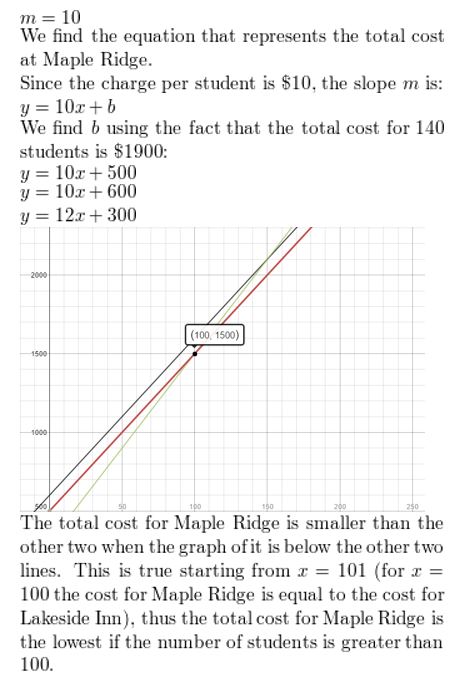
WHAT IF? Maple Ridge charges a rental fee plus a $ten fee per pupil. The full cost is $1900 for 140 students. Draw the number of students that must attend for the total cost at Maple Ridge to be less than the full costs at the other 2 venues. Use a graph to justify your answer.

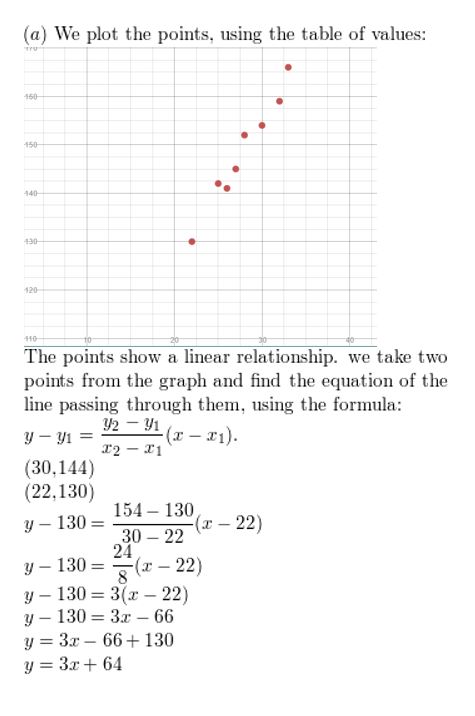
Question 3.
The tabular array shows the humerus lengths (in centimeters) and heights (in centimeters) of several females.

a. Practice the data show a linear relationship? If so, write an equation of a line of fit and use it to judge the height of a female whose humerus is forty centimeters long.
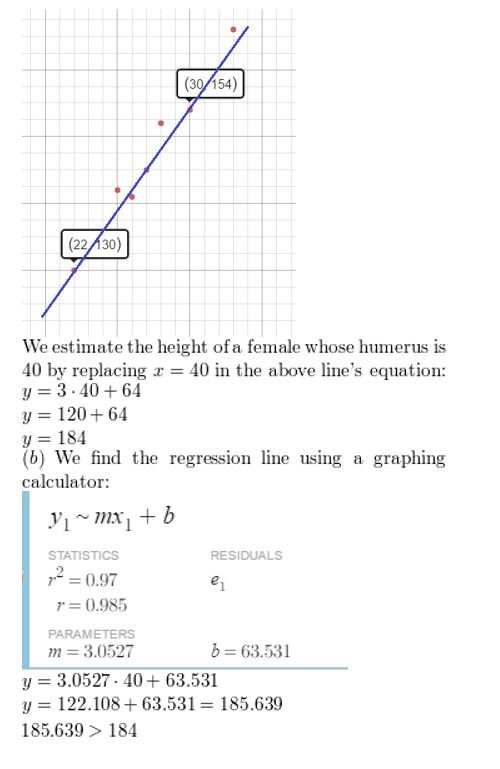
b. Apply the linear regression feature on a graphing calculator to detect an equation of the line of best fit for the information. Gauge the peak of a female whose humerus is 40 centimeters long. Compare this elevation to your estimate in role (a).

Modeling with Linear Functions one.3 Exercises

Question 1.
Complete THE SENTENCE The linear equation y = \(\frac{1}{ii}\)x + 3 is written in ____________ grade.
Answer:

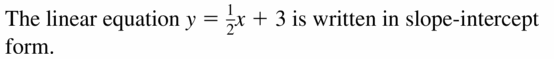
Question 2.
VOCABULARY A line of all-time fit has a correlation coefficient of -0.98. What can you conclude most the slope of the line?
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3–8, use the graph to write an equation of the line and translate the slope.

Question three.

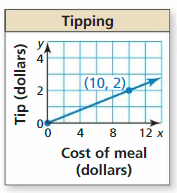
Respond:

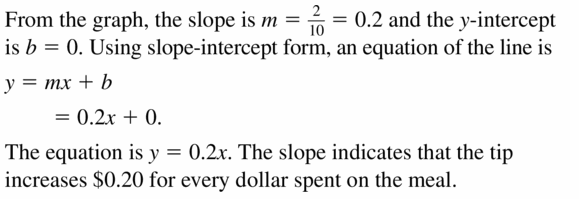
Question iv.

Answer:

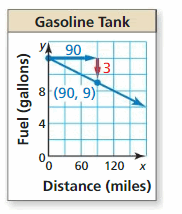
Question five.

Answer:

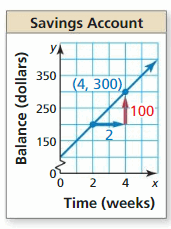
Question vi.

Answer:

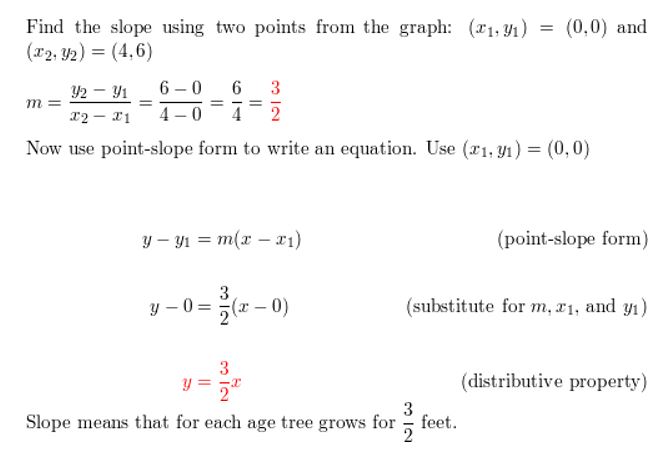
Question 7.

Reply:

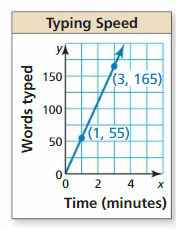
Question 8.

Respond:

Question 9.
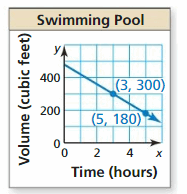
MODELING WITH MATHEMATICS Two newspapers accuse a fee for placing an advertisement in their paper plus a fee based on the number of lines in the advertisement. The tabular array shows the full costs for different length advertisements at the Daily Times. The total price y (in dollars) for an advertisement that is ten lines long at the Greenville Periodical is represented past the equation y = 2x + 20. Which newspaper charges less per line? How many lines must be in an advertisement for the total costs to be the same?

Answer:

Question 10.
PROBLEM SOLVING While on vacation in Canada, you discover that temperatures are reported in degrees Celsius. Yous know at that place is a linear relationship between Fahrenheit and Celsius, but you forget the formula. From science class, you remember the freezing indicate of water is 0°C or 32°F, and its humid point is 100°C or 212°F.
a. Write an equation that represents degrees Fahrenheit in terms of degrees Celsius.
b. The temperature exterior is 22°C. What is this temperature in degrees Fahrenheit?
c. Rewrite your equation in part (a) to correspond degrees Celsius in terms of degrees Fahrenheit.
d. The temperature of the hotel puddle water is 83°F. What is this temperature in degrees Celsius?
Reply:

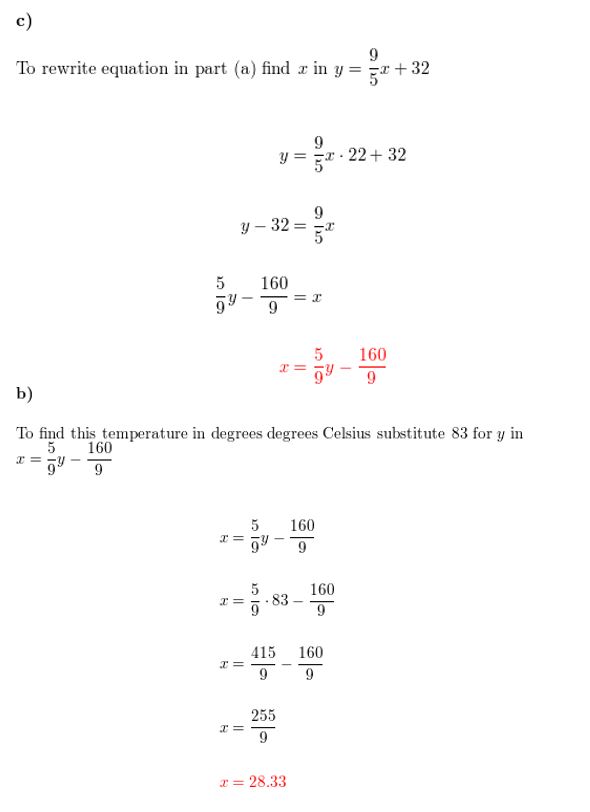
Mistake Analysis In Exercises 11 and 12, describe and correct the error in interpreting the gradient in the context of the situation.

Question eleven.

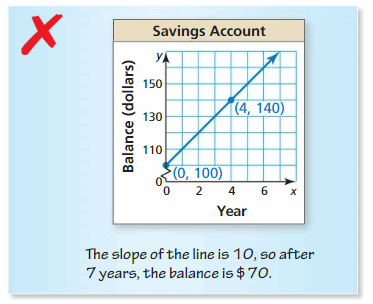
Respond:

Question 12.

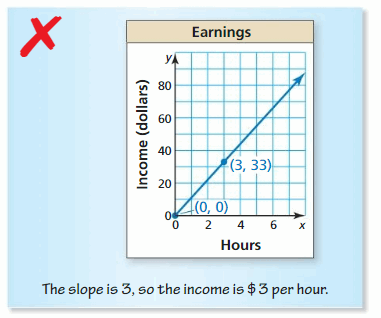
Answer:

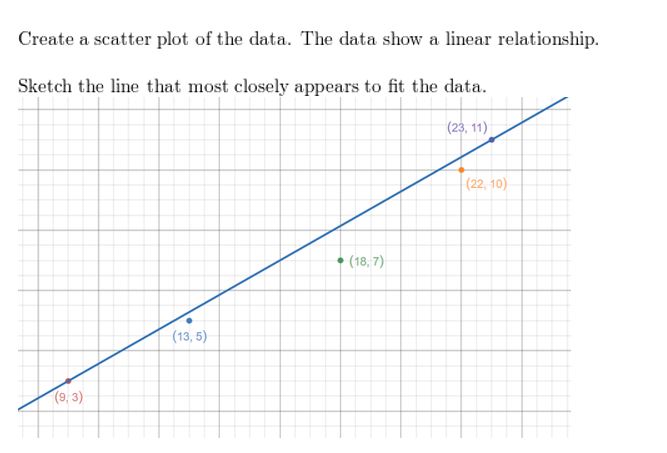
In Exercises 13–16, make up one's mind whether the data bear witness a linear relationship. If and then, write an equation of a line of fit. Estimate y when x = fifteen and explain its meaning in the context of the situation.

Question thirteen.

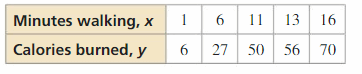
Answer:

Question fourteen.

Answer:

Question 15.

Answer:

Question sixteen.

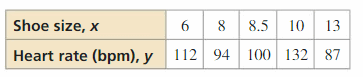
Answer:

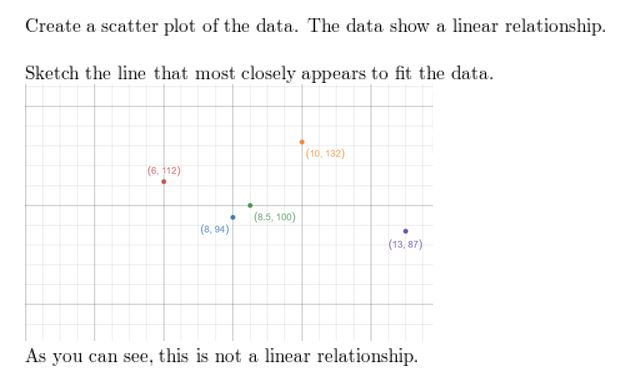
Question 17.
MODELING WITH MATHEMATICS The data pairs (x, y) correspond the average annual tuition y (in dollars) for public colleges in the Usa x years later on 2005. Employ the linear regression feature on a graphing computer to detect an equation of the line of best fit. Estimate the average almanac tuition in 2020. Translate the slope and y-intercept in this situation.

Answer:

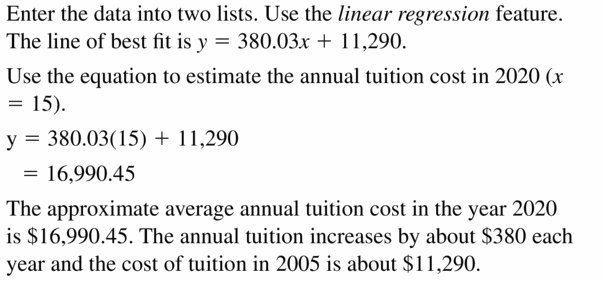
Question eighteen.
MODELING WITH MATHEMATICS The table shows the numbers of tickets sold for a concert when different prices are charged. Write an equation of a line of fit for the data. Does it seem reasonable to employ your model to predict the number of tickets sold when the ticket cost is $85? Explicate.

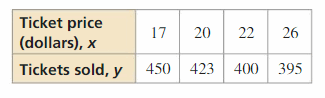
Answer:

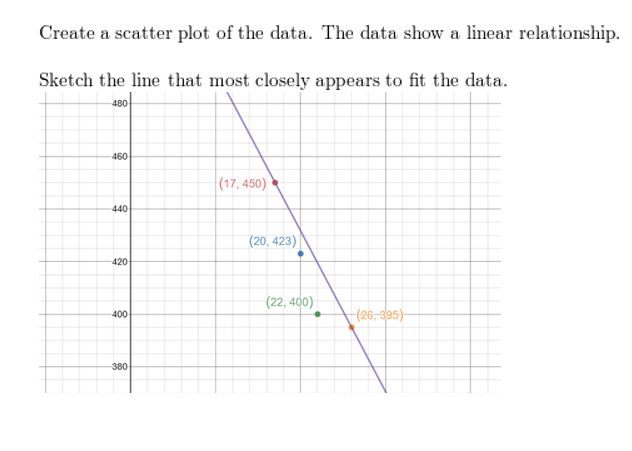
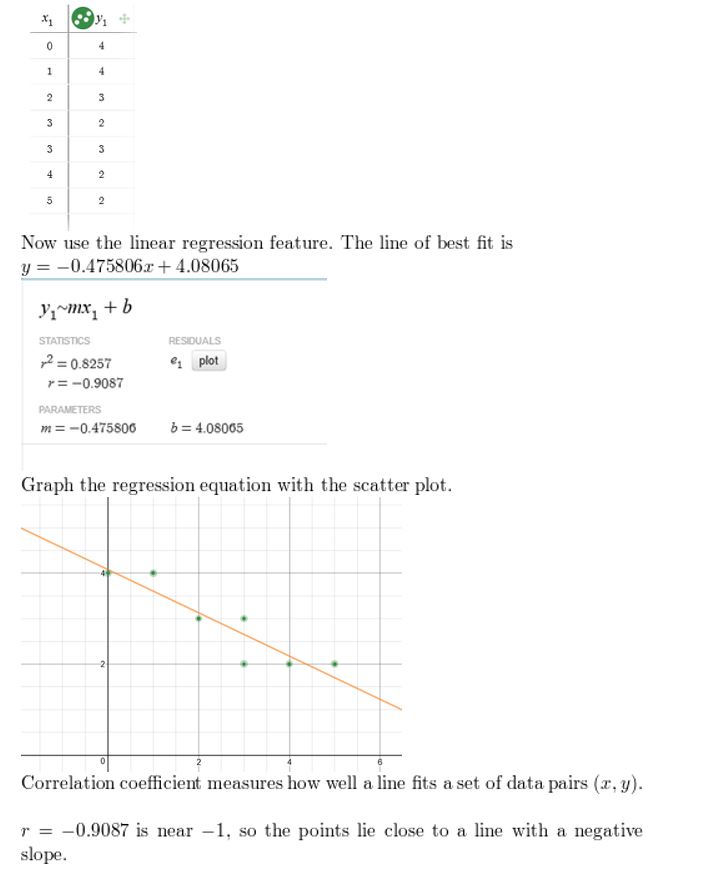
USING TOOLS In Exercises 19–24, employ the linear regression characteristic on a graphing reckoner to find an equation of the line of best fit for the data. Find and interpret the correlation coefficient.

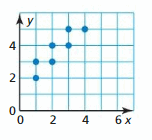
Question 19.

Respond:

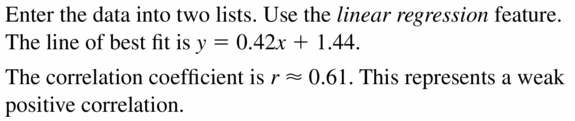
Question xx.

Respond:

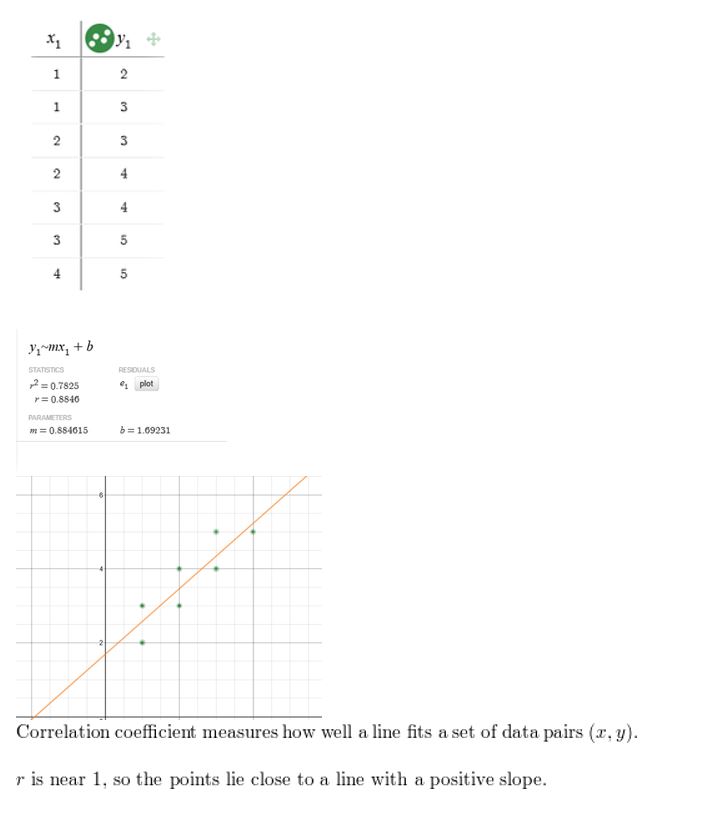
Question 21.

Respond:

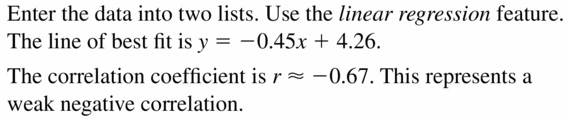
Question 22.

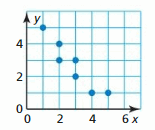
Answer:

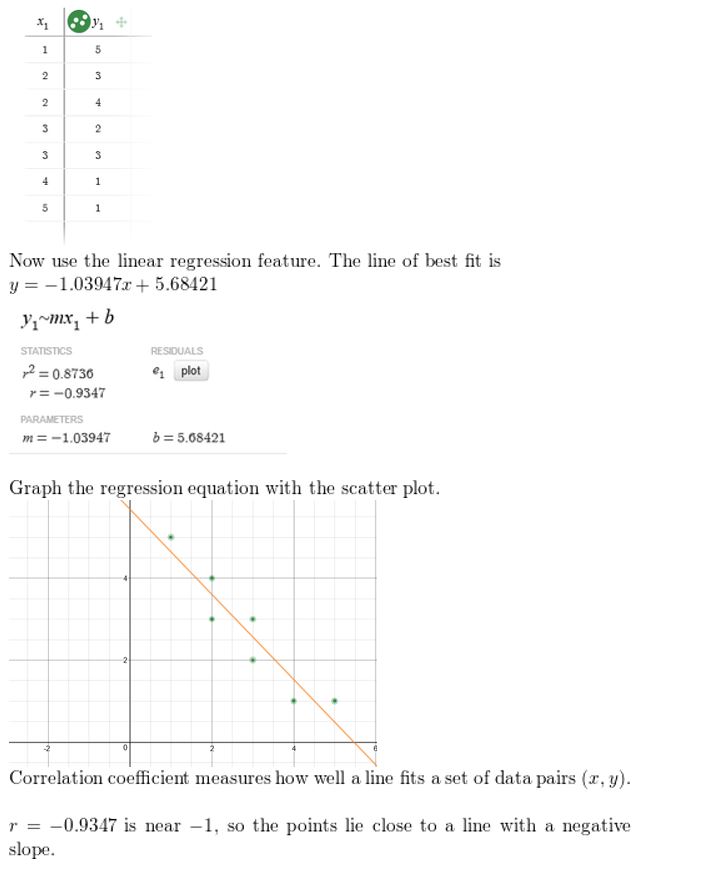
Question 23.

Answer:

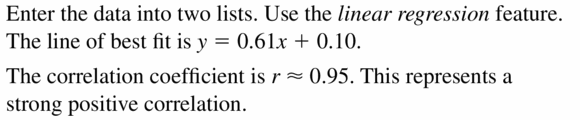
Question 24.

Respond:

Question 25.
Open up-Concluded Give two real-life quantities that have
(a) a positive correlation,
(b) a negative correlation, and
(c) approximately no correlation. Explain.
Answer:

Question 26.
HOW Exercise YOU Come across Information technology? You secure an interest-free loan to purchase a boat. Y'all concur to make equal monthly payments for the next two years. The graph shows the corporeality of money you however owe.

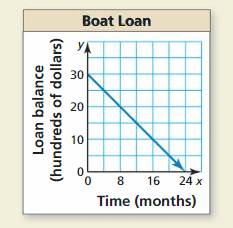
a. What is the slope of the line? What does the gradient represent?
b. What is the domain and range of the office? What does each represent?
c. How much do you lot still owe afterward making payments for 12 months?
Reply:

Question 27.
MAKING AN Argument A set of information pairs has a correlation coefficient r = 0.iii. Your friend says that because the correlation coefficient is positive, information technology is logical to utilize the line of best fit to brand predictions. Is your friend correct? Explain your reasoning.
Answer:


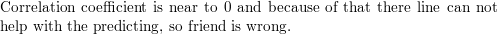
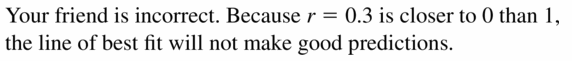
Question 28.
THOUGHT PROVOKING Points A and B lie on the line y = -x + 4. Choose coordinates for points A, B, and C where point C is the aforementioned altitude from point A equally information technology is from point B. Write equations for the lines connecting points A and C and points B and C.
Respond:

Question 29.
Abstract REASONING If x and y accept a positive correlation, and y and z take a negative correlation, and then what can y'all conclude about the correlation between x and z? Explicate.
Respond:

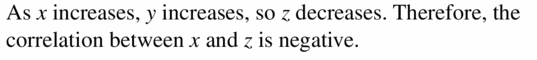
Question thirty.
MATHEMATICAL CONNECTIONS Which equation has a graph that is a line passing through the signal (8, -v) and is perpendicular to the graph of y = -4x + 1?
A. y = \(\frac{i}{4}\)ten – v
B. y = -4x + 27
C. y = –\(\frac{one}{4}\)ten – 7
D. y = \(\frac{1}{4}\)x – 7
Answer:

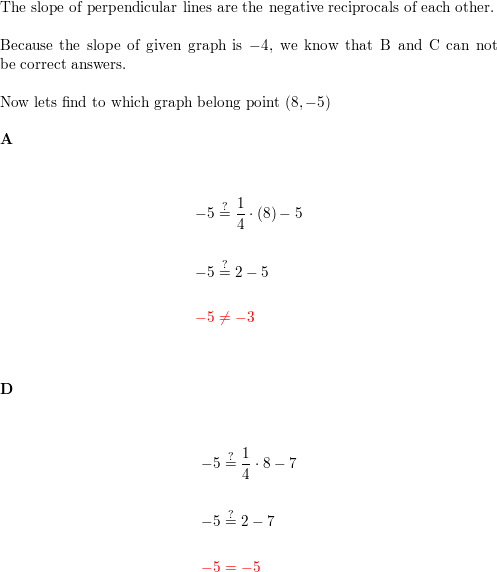
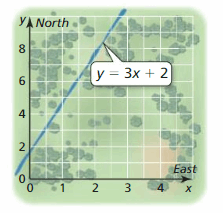
Question 31.
PROBLEM SOLVING Y'all are participating in an orienteering competition. The diagram shows the position of a river that cuts through the woods. Yous are currently 2 miles east and 1 mile north of your starting point, the origin. What is the shortest distance you must travel to reach the river?

Answer:

Question 32.
ANALYZING RELATIONSHIPS Data from North American countries show a positive correlation between the number of personal computers per capita and the average life expectancy in the state.
a. Does a positive correlation make sense in this situation? Explicate.
b. Is information technology reasonable to conclude that giving residents of a state personal computers will lengthen their lives? Explain.

Answer:

Maintaining Mathematical Proficiency

Solve the system of linear equations in two variables past elimination or substitution. (Skills Review Handbook)

Question 33.
3x + y = 7
-2x – y = ix
Answer:

Question 34.
4x + 3y = 2
2x – 3y = 1
Reply:

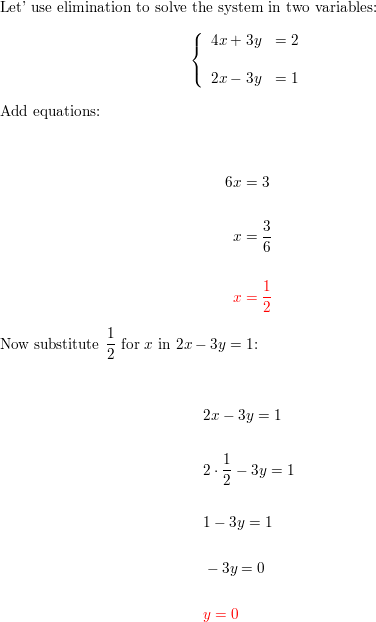
Question 35.
2x + 2y = 3
x = 4y – one
Reply:

Question 36.
y = 1 + x
2x + y = -2
Reply:

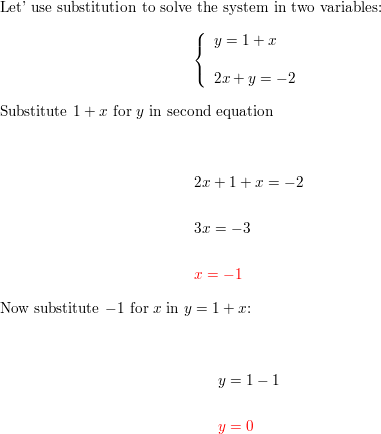
Question 37.
\(\frac{ane}{2}\)10 + 4y = 4
2x – y = one
Answer:

Question 38.
y = x – 4
4x + y = 26
Answer:

Lesson 1.four Solving Linear Systems

Essential Question
How can y'all decide the number of solutions of a linear arrangement?
A linear system is consequent when it has at to the lowest degree i solution. A linear organization is inconsistent when it has no solution.

EXPLORATION i
Recognizing Graphs of Linear Systems
Work with a partner. Match each linear system with its respective graph. Explain your reasoning. Then classify the system as consistent or inconsistent.
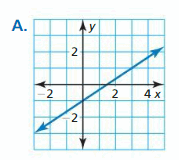
a. 2x – 3y = iii
-4x + 6y = 6

b. 2x – 3y = iii
ten + 2y = 5

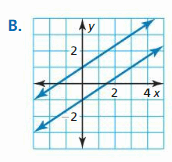
c. 2x – 3y = 3
-4x + 6y = vi

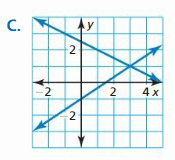
EXPLORATION 2
Solving Systems of Linear Equations
Work with a partner. Solve each linear arrangement by substitution or elimination. Then use the graph of the system below to cheque your solution.
a. 2x + y = five
x – y = 1

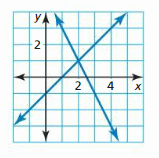
b. x+ 3y = ane
-10 + 2y = four

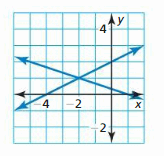
c. x + y = 0
3x + 2y = ane

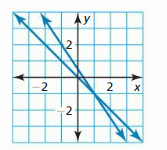
Communicate Your Answer

Question iii.
How can you make up one's mind the number of solutions of a linear system?

Question 4.
Suppose you were given a organization of three linear equations in 3 variables. Explicate how you would arroyo solving such a system.

Question five.
Apply your strategy in Question 4 to solve the linear system.

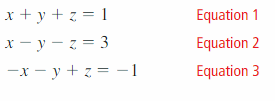
1.four Lesson

Monitoring Progress

Question ane.
x – 2y + z = -xi
3x + 2y – z = vii
-ten + 2y + 4z = -nine

Question 2.
x + y – z = -ane
4x + 4y – 4z = -2
3x + 2y + z = 0

Question 3.
x + y + z = 8
ten – y + z = eight
2x + y + 2z = 16

Question 4.
In Example 3, describe the solutions of the arrangement using an ordered triple in terms of y.

Question 5.
WHAT IF? On the beginning solar day, ten,000 tickets sold, generating $356,000 in revenue. The number of seats sold in Sections A and B are the aforementioned. How many lawn seats are still available?

Solving Linear Systems 1.four Exercises

Vocabulary and Core Concept Bank check

Question 1.
VOCABULARY The solution of a system of three linear equations is expressed as a(north)__________.
Answer:

Question 2.
WRITING Explain how you know when a linear system in three variables has infinitely many solutions.
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises three–eight, solve the organisation using the elimination method.

Question 3.
ten + y – 2z = five
-x + 2y + z = 2
2x + 3y – z = ix
Answer:

Question 4.
x + 4y – 6z = -ane
2x – y + 2z = -7
-ten + 2y – 4z = 5
Answer:

Question 5.
2x + y – z = ix
-x + 6y + 2z = -17
5x + 7y + z = 4
Respond:

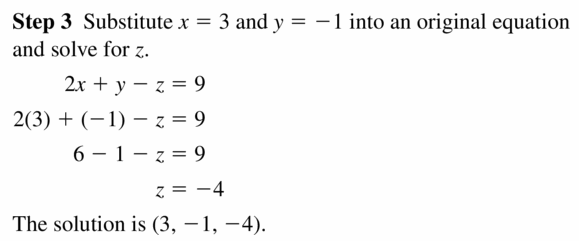
Question vi.
3x + 2y – z = 8
-3x + 4y + 5z = -14
x – 3y + 4z = -fourteen

Answer:

Question 7.
2x + 2y + 5z = -ane
2x – y + z = 2
2x + 4y – 3z = xiv
Answer:

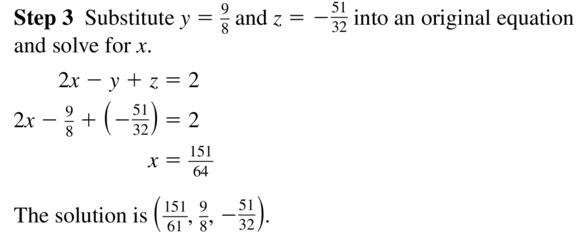
Question 8.
3x + 2y – 3z = -2
7x – 2y + 5z = -14
2x + 4y + z = 6
Answer:

Fault ANALYSIS In Exercises nine and ten, depict and correct the error in the first step of solving the system of linear equations.

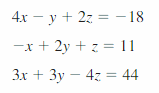
Question 9.

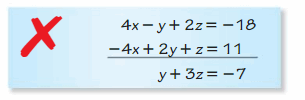
Answer:

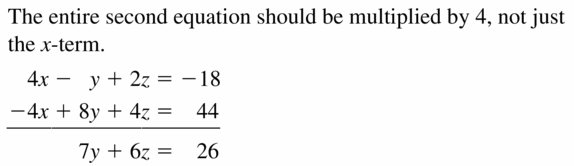
Question 10.

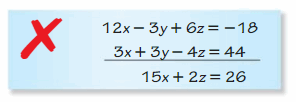
Reply:

In Exercises 11–xvi, solve the organization using the emptying method.

Question 11.
3x – y + 2z = 4
6x – 2y + 4z = -viii
2x – y + 3z = ten
Answer:

Question 12.
5x + y – z = 6
x + y + z = ii
12x + 4y = 10
Answer:

Question 13.
x + 3y – z = 2
x + y – z = 0
3x + 2y – 3z = -1
Respond:

Question 14.
10 + 2y – z = 3
-2x – y + z = -1
6x – 3y – z = -vii
Answer:

Question 15.
x + 2y + 3z = 4
-3x + 2y – z = 12
-2x – 2y – 4z = -14
Answer:

Question 16.
-2x – 3y + z = -half dozen
x + y – z = v
7x + 8y – 6z = 31
Answer:

Question 17.
MODELING WITH MATHEMATICS 3 orders are placed at a pizza shop. Two small pizzas, a liter of soda, and a salad price $14; one small pizza, a liter of soda, and three salads cost $15; and iii small pizzas, a liter of soda, and ii salads cost $22. How much does each particular cost?

Answer:

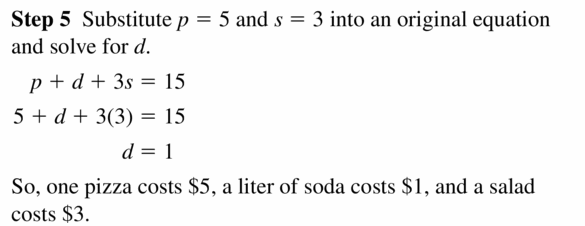
Question 18.
MODELING WITH MATHEMATICS Sam'southward Furniture Store places the following advertisement in the local newspaper. Write a organisation of equations for the three combinations of furniture. What is the cost of each piece of furniture? Explain.

Answer:

In Exercises 19–28, solve the system of linear equations using the substitution method.

Question 19.
-2x + y + 6z = 1
3x + 2y + 5z = xvi
7x + 3y – 4z = 11
Reply:

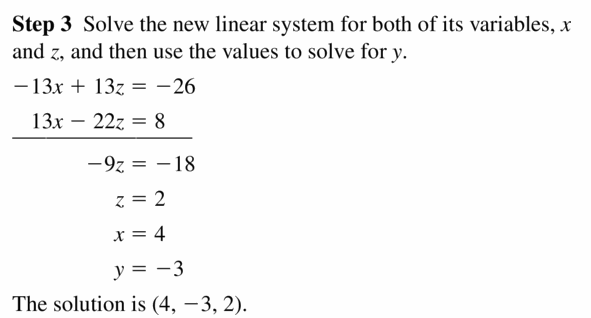
Question xx.
x – 6y – 2z = -eight
-x + 5y + 3z = 2
3x – 2y – 4z = 18
Respond:

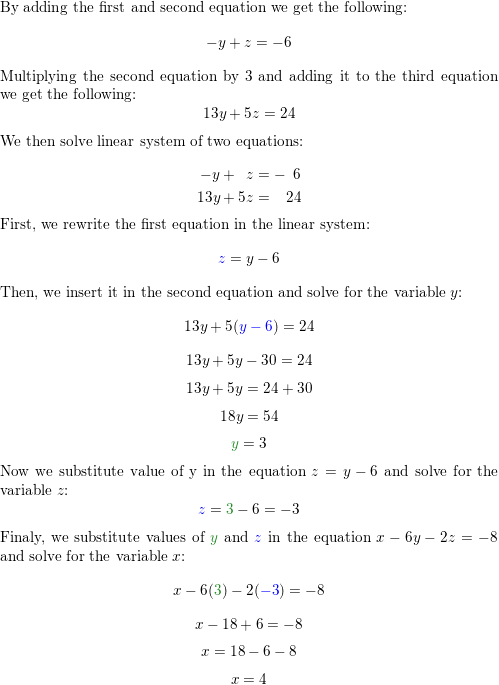
Question 21.
x + y + z = 4
5x + 5y + 5z = 12
x – 4y + z = 9
Reply:

Question 22.
x + 2y = -1
-x + 3y + 2z = -4
-x + y – 4z = 10
Respond:

Question 23.
2x – 3y + z = 10
y + 2z = 13
z = 5
Answer:

Question 24.
x = 4
x + y = -6
4x – 3y + 2z = 26
Answer:

Question 25.
x + y – z = 4
3x + 2y + 4z = 17
-x + 5y + z = 8
Answer:

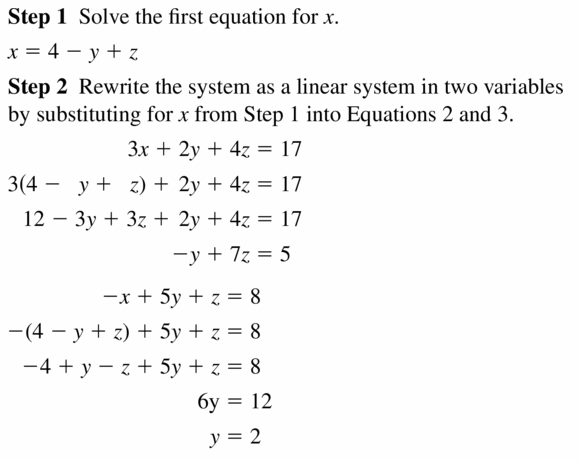
Question 26.
2x – y – z = 15
4x + 5y + 2z = 10
-ten – 4y + 3z = -20
Respond:

Question 27.
4x + y + 5z = 5
8x + 2y + 10z = 10
x – y – 2z = -ii
Answer:

Question 28.
x + 2y – z = iii
2x + 4y – 2z = vi
-10 – 2y + z = -vi
Answer:

Question 29.
PROBLEM SOLVING The number of left-handed people in the globe is i-tenth the number of right-handed people. The percent of right-handed people is nine times the percentage of left-handed people and ambidextrous people combined. What percent of people are ambidextrous?

Answer:

Question 30.
MODELING WITH MATHEMATICS Use a organisation of linear equations to model the information in the following newspaper article. Solve the organisation to observe how many athletes finished in each identify.

Answer:

Question 31.
WRITING Explain when it might be more convenient to apply the elimination method than the exchange method to solve a linear arrangement. Give an example to support your claim.
Answer:

Question 32.
REPEATED REASONING Using what y'all know about solving linear systems in ii and three variables, plan a strategy for how yous would solve a system that has four linear equations in four variables.
Answer:

MATHEMATICAL CONNECTIONS In Exercises 33 and 34, write and utilise a linear system to answer the question.

Question 33.
The triangle has a perimeter of 65 feet. What are the lengths of sides ℓ, m, and n?

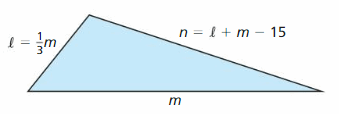
Answer:

Question 34.
What are the measures of angles A, B, and C?

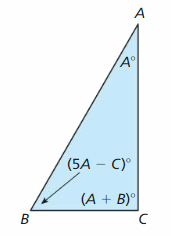
Answer:

Question 35.
Open up-ENDED Consider the system of linear equations beneath. Cull nonzero values for a, b, and c so the system satisfies the given status. Explain your reasoning.
x + y + z = 2
ax + by + cz = 10
x – 2y + z = 4
a. The arrangement has no solution.
b. The system has exactly ane solution.
c. The system has infinitely many solutions.
Answer:

Question 36.
MAKING AN Argument A linear system in three variables has no solution. Your friend concludes that it is non possible for two of the three equations to have whatever points in common. Is your friend correct? Explain your reasoning.
Answer:

Question 37.
Trouble SOLVING A contractor is hired to build an apartment complex. Each 840-square-pes unit of measurement has a bedroom, kitchen, and bathroom. The sleeping accommodation will be the aforementioned size as the kitchen. The owner orders 980 foursquare feet of tile to completely cover the floors of two kitchens and ii bathrooms. Determine how many square feet of carpet is needed for each bedchamber.

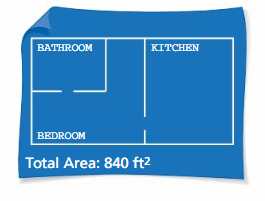
Answer:

Question 38.
Idea PROVOKING Does the system of linear equations accept more than than i solution? Justify your answer.
4x + y + z = 0
2x + \(\frac{i}{2}\)y – 3z = 0
-x – \(\frac{one}{4}\)y – z = 0
Answer:

Question 39.
Trouble SOLVING A florist must make 5 identical bridesmaid bouquets for a wedding. The budget is $160, and each bouquet must have 12 flowers. Roses cost $two.50 each, lilies cost $four each, and irises cost $ii each. The florist wants twice as many roses as the other two types of flowers combined.
a. Write a system of equations to represent this situation, assuming the florist plans to apply the maximum budget.
b. Solve the system to discover how many of each type of flower should be in each bouquet.
c. Suppose at that place is no limitation on the full cost of the bouquets. Does the problem still have exactly one solution? If then, find the solution. If not, give three possible solutions.
Answer:

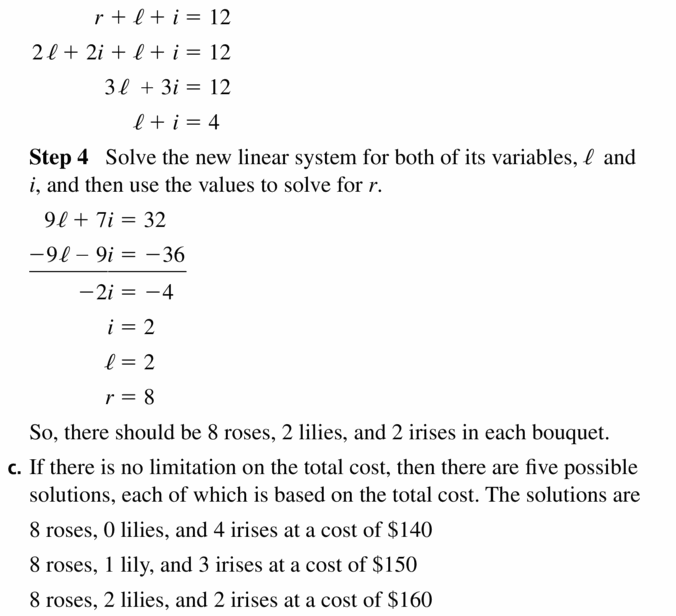
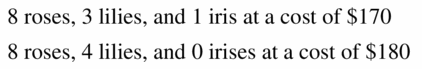
Question 40.
HOW DO YOU Come across Information technology? Determine whether the system of equations that represents the circles has no solution, one solution, or infinitely many solutions. Explicate your reasoning.

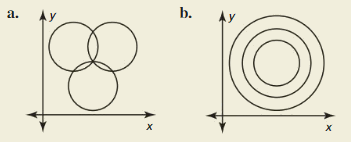
Answer:

Question 41.
CRITICAL THINKING Find the values of a, b, and c and then that the linear system shown has (-one, 2, -3) as its but solution. Explain your reasoning.
x + 2y – 3z = a
– x – y + z = b
2x + 3y – 2z = c
Answer:

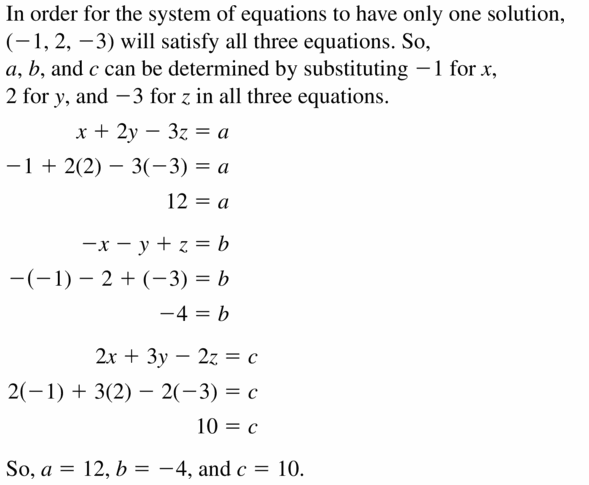
Question 42.
ANALYZING RELATIONSHIPS Determine which arrangement(due south) of the integers -5, two, and three produce a solution of the linear system that consist of only integers. Justify your answer.
x – 3y + 6z = 21
_x + _y + _z = -thirty
2x – 5y + 2z = -half-dozen
Answer:

Question 43.
ABSTRACT REASONING Write a linear arrangement to represent the first three pictures below. Use the system to determine how many tangerines are required to residual the apple in the fourth pic. Notation:The beginning picture shows that one tangerine and ane apple tree balance 1 grapefruit.

Answer:

Maintaining Mathematical Proficiency

Simplify. (Skills Review Handbook)

Question 44.
(ten – two)²

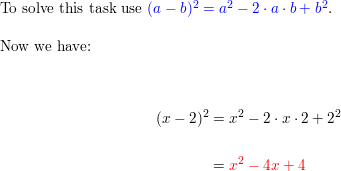
Answer:

Question 45.
(3m + 1)²

Respond:

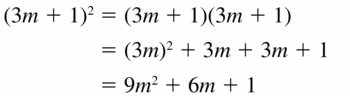
Question 46.
(2z – 5)²

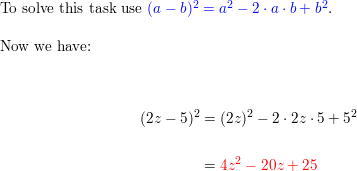
Respond:

Question 47.
(iv – y)²

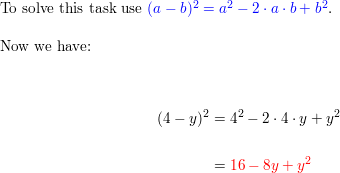
Respond:

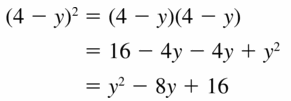
Write a office chiliad described by the given transformation of f(x) =∣ten∣− v.(Section 1.two)

Question 48.
translation ii units to the left
Reply:

Question 49.
reflection in the x-axis
Answer:

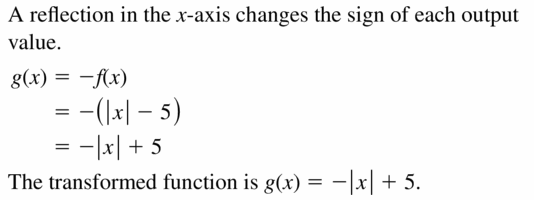
Question 50.
translation iv units up
Respond:

Question 51.
vertical stretch by a cistron of three
Answer:

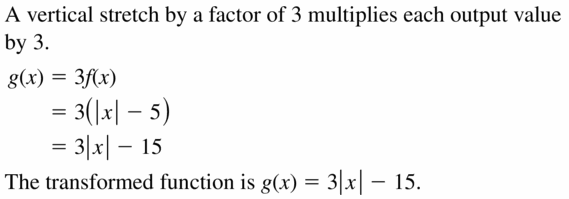
Linear Functions Performance Task: Hugger-mugger of the Hanging Baskets

one.3–one.four What Did You Learn?

Core Vocabulary

Cadre Concepts
Section 1.3
Writing an Equation of a Line, p. 22
Finding a Line of Fit, p. 24
Section 1.iv
Solving a 3-Variable Arrangement, p. 31
Solving Real-Life Problems, p. 33

Mathematical Practices

Question 1.
Describe how y'all can write the equation of the line in Exercise 7 on page 26 using but ane of the labeled points.

Question 2.
How did yous utilize the data in the newspaper article in Practice 30 on page 35 to write a arrangement of three linear equations?

Question three.
Explain the strategy yous used to cull the values for a, b, and c in Exercise 35 function (a) on page 35.

Performance Task

Secret of the Hanging Baskets
A carnival game uses two baskets hanging from springs at different heights. Next to the higher basket is a pile of baseballs. Adjacent to the lower basket is a pile of golf game balls. The object of the game is to add the aforementioned number of balls to each basket so that the baskets have the same height. But in that location is a catch—you just become one chance. What is the underground to winning the game?

To explore the answers to this question and more, go to BigIdeasMath.com.

Linear Functions Chapter Review

Graph the function and its parent function. And then describe the transformation.

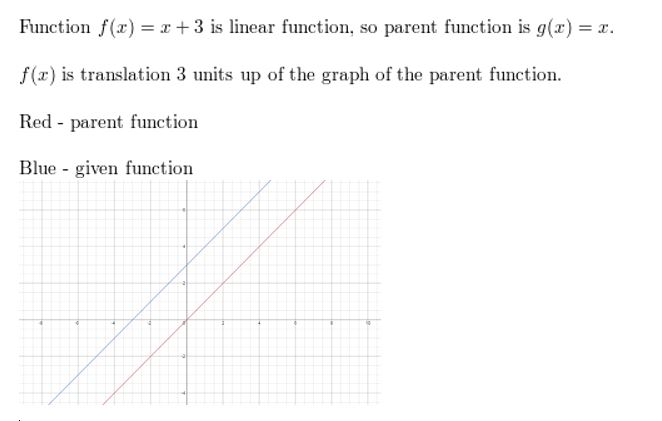
Question 1.
f(x) = 10 + three

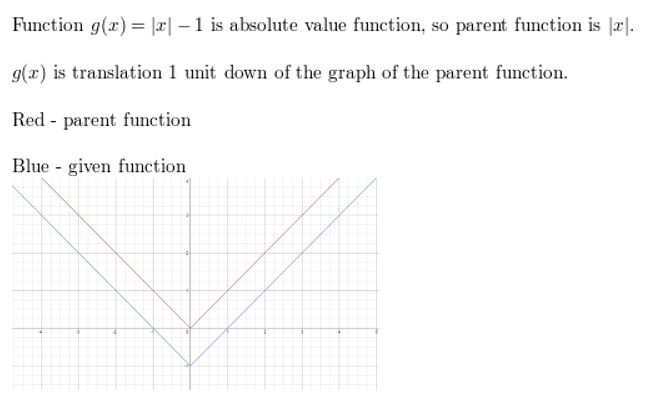
Question ii.
one thousand(x) = | x | – 1

Question iii.
h(ten) = \(\frac{1}{2}\)10^two

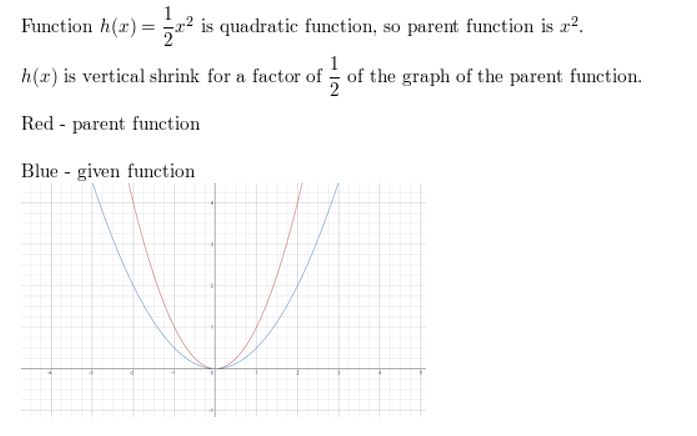
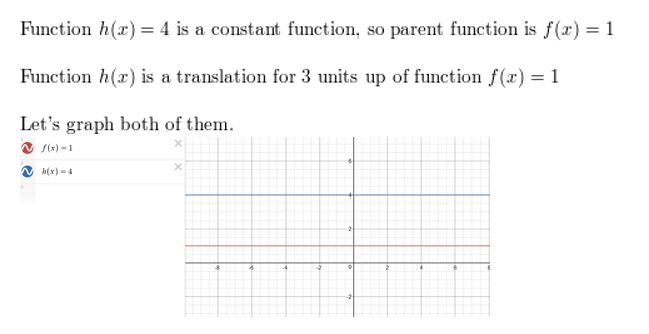
Question 4.
h(x) = 4

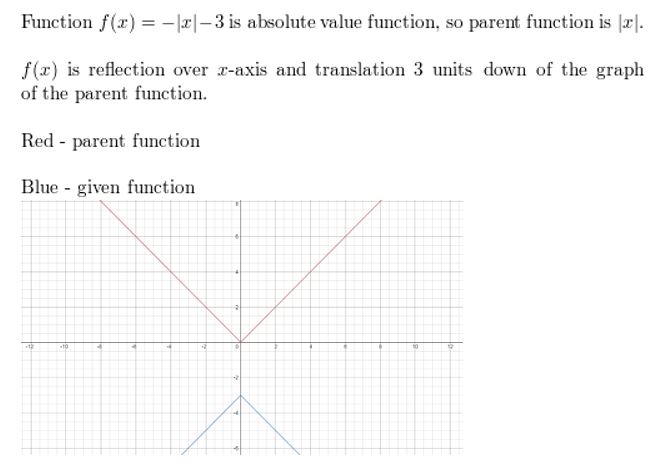
Question 5.
f(x) = -| 10 | – 3

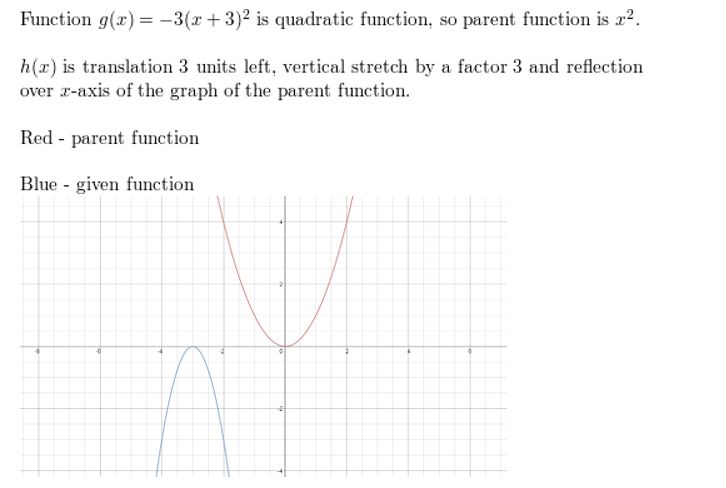
Question half-dozen.
chiliad(x) = -3(x + 3)²

Write a function grand whose graph represents the indicated transformations of the graph of f. Use a graphing calculator to bank check your answer.

Question 7.
f(10) = | 10 |; reflection in the x-axis followed by a translation 4 units to the left

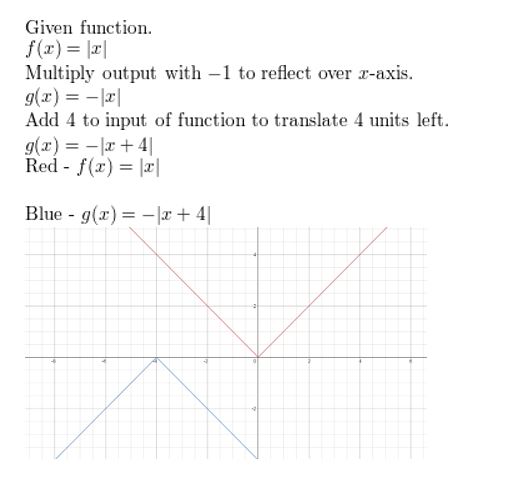
Question 8.
f(x) = | x | ; vertical shrink by a gene of \(\frac{ane}{2}\) followed by a translation ii units upwards

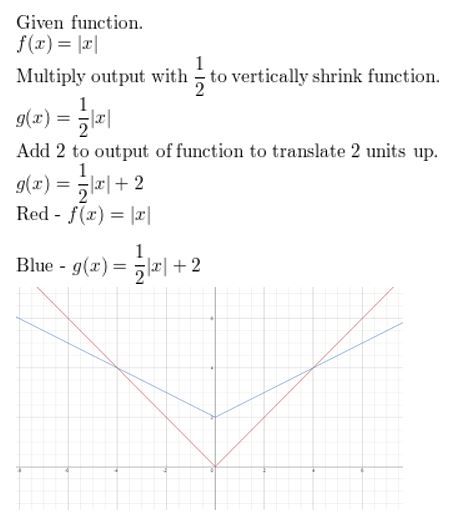
Question 9.
f(x) = 10; translation 3 units down followed by a reflection in the y-centrality

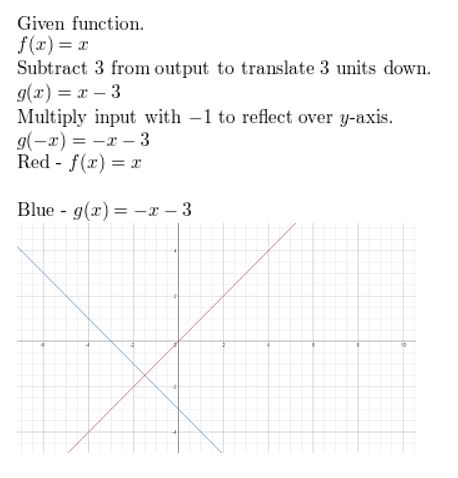
Question 10.
The tabular array shows the total number y (in billions) of U.Southward. movie admissions each twelvemonth for 10 years. Utilise a graphing calculator to notice an equation of the line of best fit for the information.

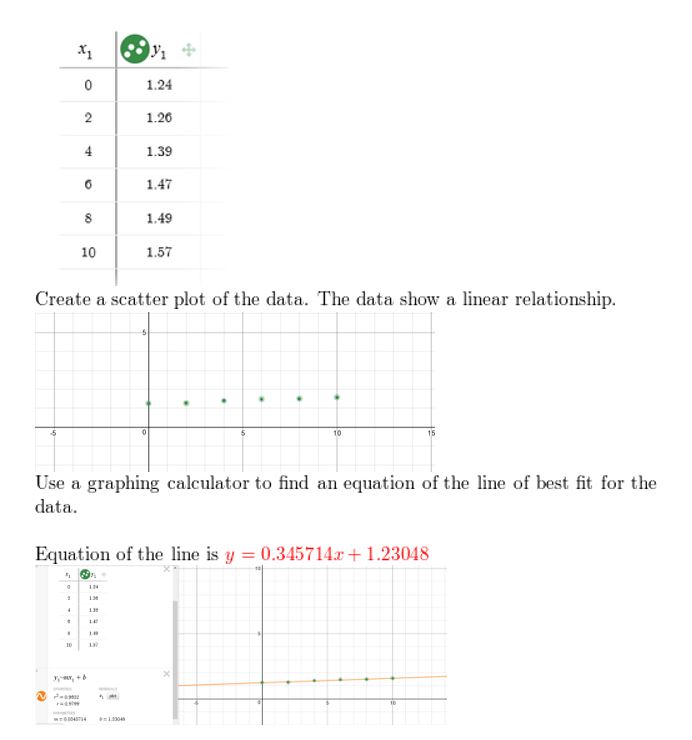
Question 11.
You ride your bike and measure out how far y'all travel. After ten minutes, y'all travel three.5 miles. After 30 minutes, you travel 10.v miles. Write an equation to model your distance. How far can you ride your cycle in 45 minutes?

Question 12.
x + y + z = iii
-10 + 3y + 2z = -viii
x = 4z

Question thirteen.
2x – 5y – z = 17
ten + y + 3z = 19
-4x + 6y + z = -20

Question xiv.
x + y + z = ii
2x – 3y + z = 11
-3x + 2y – 2z = -13

Question fifteen.
x + 4y – 2z = 3
10 + 3y + 7z = one
2x + 9y – 13z = 2

Question sixteen.
x – y + 3z = 6
ten – 2y = five
2x – 2y + 5z = 9

Question 17.
x + 2y = 4
x + y + z = half-dozen
3x + 3y + 4z = 28

Question eighteen.
A school ring performs a jump concert for a crowd of 600 people. The revenue for the concert is $3150. In that location are 150 more than adults at the concert than students. How many of each blazon of ticket are sold?

Linear Functions Chapter Test

Write an equation of the line and interpret the slope and y-intercept.

Question 1.

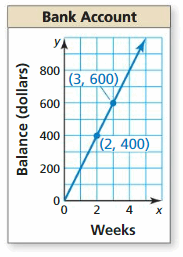
Question ii.

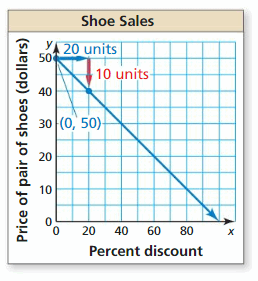
Solve the arrangement. Check your solution, if possible.

Question 3.
-2x + y + 4z = 5
x + 3y – z = two
4x + y – 6z = 11

Question 4.
y = \(\frac{ane}{2}\)z
x + 2y + 5z = 2
3x + 6y – 3z = 9

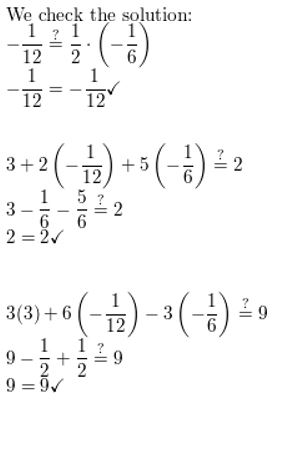
Question five.
ten – y + 5z = 3
2x + 3y – z = ii
-4x – y – 9z = -eight

Graph the function and its parent function. Then describe the transformation.

Question six.

Question eight.
f(x) = iv

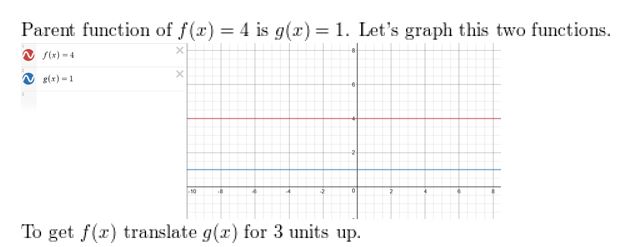
Match the transformation of f(x) = x with its graph. And then write a dominion for yard.

Question 9.
g(10) = 2f(x) + 3

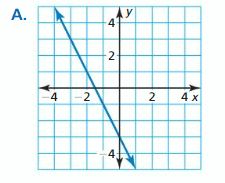
Question ten.
g(x) = 3f(x) – 2

Question 11.
g(x) = -2f(x) – 3

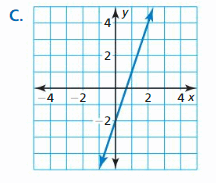
Question 12.
A bakery sells doughnuts, muffins, and bagels. The baker makes three times every bit many doughnuts as bagels. The baker earns a full of $150 when all 130 baked items in stock are sold. How many of each item are in stock? Justify your answer.

Question 13.
A fountain with a depth of 5 feet is drained and then refilled. The water level (in feet) after t minutes can be modeled by f(t) = \(\frac{1}{four}\)|t – twenty |. A 2nd fountain with the same depth is drained and filled twice as quickly as the starting time fountain. Describe how to transform the graph of f to model the water level in the 2nd fountain after t minutes. Find the depth of each fountain after 4 minutes. Justify your answers.

Linear Functions Cumulative Cess

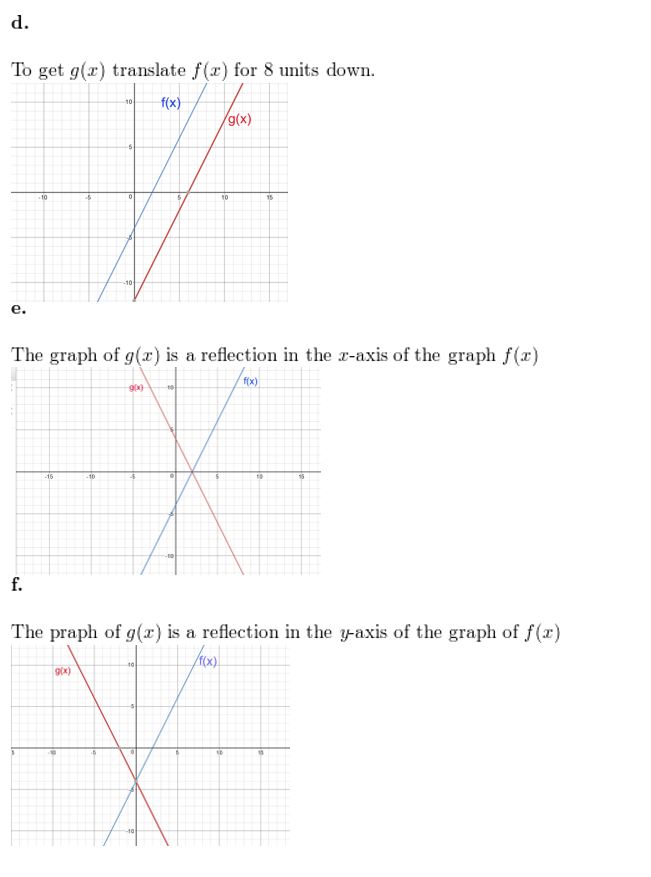
Question 1.
Describe the transformation of the graph of f(x) = 2x – 4 represented in each graph.

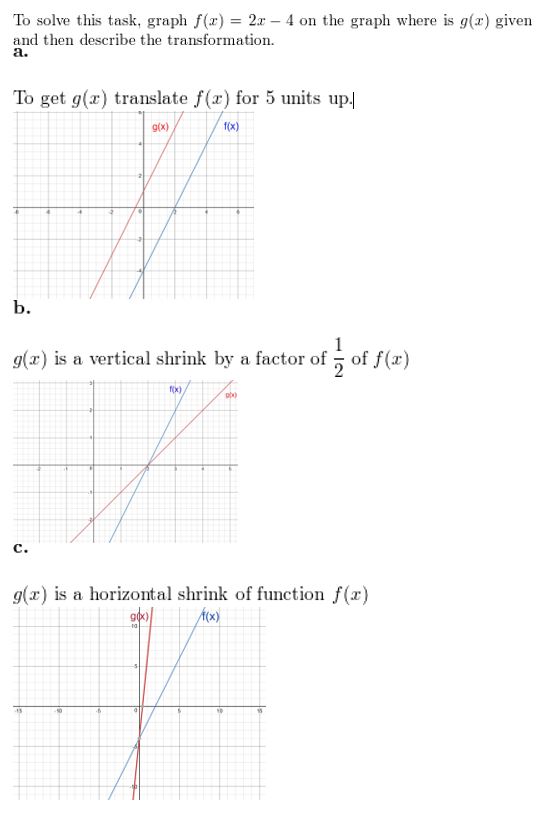
Question 2.
The table shows the tuition costs for a private school between the years 2010 and 2013.

a. Verify that the data show a linear relationship. Then write an equation of a line of fit.
b. Interpret the slope and y-intercept in this situation.
c. Predict the cost of tuition in 2015.

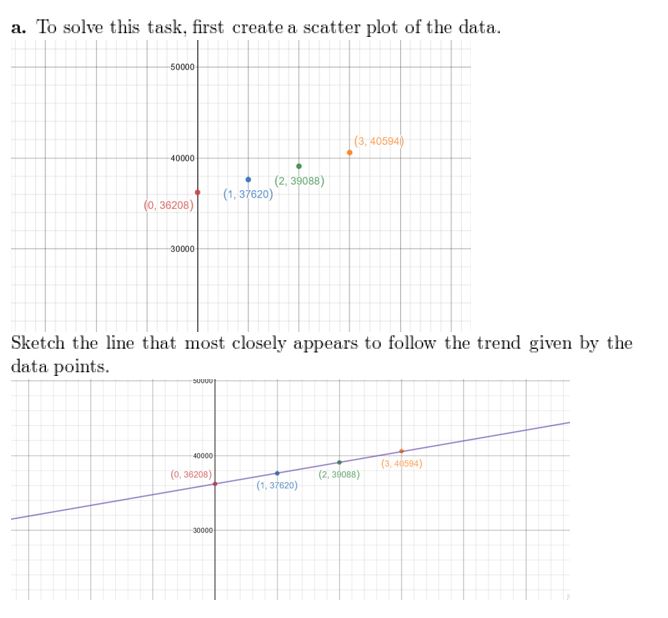
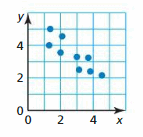
Question 3.
Your friend claims the line of best fit for the data shown in the scatter plot has a correlation coefficient close to 1. Is your friend correct? Explain your reasoning.

Question 4.
Order the post-obit linear systems from least to greatest co-ordinate to the number of solutions.
A. 2x + 4y – z = 7
14x + 28y – 7z = 49
-x + 6y + 12z = 13
B. 3x – 3y + 3z = 5
-10 + y – z = five
-10 + y – z = 8
14x – 3y + 12z = 108
C. 4x – y + 2z = 18
-x + 2y + z = xi
3x + 3y – 4z = 44

Question 5.
Y'all make a DVD of three types of shows: one-act, drama, and reality-based. An episode of a comedy lasts xxx minutes, while a drama and a reality-based episode each last 60 minutes. The DVDs can concord 360 minutes of programming.
a. You completely fill a DVD with seven episodes and include twice as many episodes of a drama as a one-act. Create a system of equations that models the situation.
b. How many episodes of each type of show are on the DVD in role (a)?
c. You completely make full a second DVD with only six episodes. Practise the 2 DVDs take a dissimilar number of comedies? dramas? reality-based episodes? Explain.

Question six.
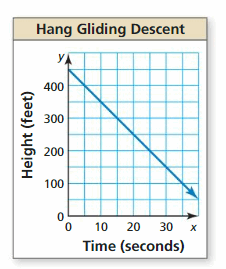
The graph shows the height of a hang glider over time. Which equation models the situation?
A. y + 450 = 10x
B. 10y = -x+ 450
C. \(\frac{1}{10}\)y = -x + 450
D. 10x + y = 450

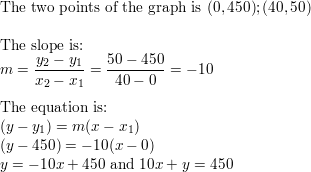
Question 7.
Let f(x) = x and grand(x) = -3x – iv. Select the possible transformations (in order) of the graph of f represented past the function g.
A. reflection in the x-axis
B. reflection in the y-axis
C. vertical translation four units down
D. horizontal translation 4 units correct
E. horizontal compress by a factor of \(\frac{1}{three}\)
F. vertical stretch by a factor of 3

Question 8.
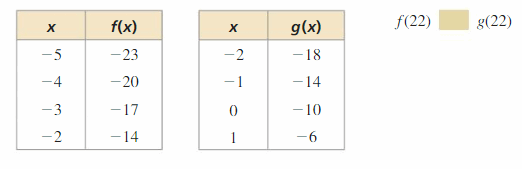
Choose the right equality or inequality symbol which completes the argument beneath about the linear functions f and m. Explicate your reasoning.

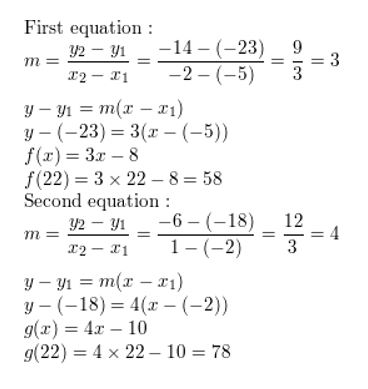
willmottluelf2001.blogspot.com

Source: https://ccssmathanswers.com/big-ideas-math-algebra-2-answers-chapter-1/

Share this post